In the last part of this 3-segment Guided Project, we introduced the concept of Exploratory Data Analysis (EDA). We made some initial data exploration and chose a set of risk factors which could be potentially used to predict the severity of a given patient’s Lung Cancer condition. We also introduced a simple business case requested by our client, an insurance company, and proceeded to analyze a data set provided.
In this section, we will go over 12 different classification algorithms. We will start by preparing our data. We will then discuss, in a very general way, the underlying theory behind each model and its assumptions. We will finally implement each method step-by-step and make a performance comparison.
We’ll use Python scripts found in the Guided Project Repo.
The generated plots and test results from the last segment can also be found in the plots and outputs folder respectively.
Classification model implementation
Classification models are a subset of supervised machine learning algorithms. A typical classification model reads an input and tries to classify it based on some predefined properties. A straightforward example would be the classification of a mail containing spam vs one without spam.
The other type of supervised algorithm, perhaps more familiar, is regression models. These differ because they don’t classify our inputs but predict continuous variables. A typical example would be predicting the stock market behaviour for a given asset.
1. Selecting our methods
We can implement multiple supervised models to try to predict the severity of Lung Cancer for a given patient. It’s always a good idea to test at least a set of different models and compare their accuracy. Since we have categorical, ordinal variables, we will test different classification algorithms.
It’s also important to consider that not every classification algorithm is appropriate for every classification problem. Each model is based on assumptions that may render it unusable for certain applications.
In this example, we will be working with 12 classification models, which we’ll explain in more detail further on:
- Multinomial Logistic Regression
- Decision Tree
- Random Forest
- Support Vector Machine
- K-Nearest Neighbors
- K-Means Clustering
- Gaussian Naïve Bayes
- Bernoulli Naïve Bayes
- Stochastic Gradient Descent
- Gradient Boosting
- Extreme Gradient Boosting
- Deep Neural Networks
2. Creating a Virtual Environment
Before anything else, we need to check our current Python version. This is important because although we’ll not be using tensorflow directly, we will require it for our Deep Neural Network model using keras, and tensorflow currently supports *Python versions 3.7 – 3.10:
Code
import sys
sys.versionOutput
'3.11.1 (tags/v3.11.1:a7a450f, Dec 6 2022, 19:58:39) [MSC v.1934 64 bit (AMD64)]'We can consult each operating system’s tensorflow installation requirements here.
If we have a Python version within the range above, we’ll be fine and can skip to the module installation part. Otherwise, we have two options:
- Install an older version of Python user-wide or system-wide, and use it as our default interpreter.
- Create a new virtual environment containing a downgraded Python version.
The second option is always best practice because another program we wrote might be using a newer Python version. If we replace our current Python version with an older one, we could break any program we wrote using more recent versions. Virtual environments handle these types of conflicts; we can have multiple Python installations and selectively choose which environment to work with, depending on each case.
Since we require a different Python version than the one we have, we will first download and install our target version by heading to the Python Releases for Windows site.
We will then select the version that we want to download. For this case, we will use Python 3.10.0 – Oct. 4, 2021 by getting the corresponding 64-bit Windows installer. Upon download, we will execute the installer and wait for it to conclude. A new Python version will be installed on our system.
Since we installed it user-wide, the executable will be found on C:/Users/our_username/AppData/Local/Programs/Python. We must remember this path since we will use it to point to the Python version upon our venv creation.
We will then create a new virtual environment dedicated to this project. For this, we will need to first cd into our project directory:
Code
cd 'C:/Users/our_username/exploratory-data-analysis'We will then create the environment using the built-in venv package. We can provide whichever name we like. Since we don’t have Python 3.10 specified in PATH, we will need to refer to it by specifying the full absolute path.
Code
C:\Users\our_username\AppData\Local\Programs\Python\Python310\python.exe -m venv 'eda_venv'We will see that a new folder was created on our working directory:
lsOutput
eda_venv
outputs
plots
cancer patient data sets.csv
exploratory-data-analysis-1.py
exploratory-data-analysis-2.pyWe can then activate our environment:
Code
cd eda_venv\Scripts
.\Activate.ps1We must remember that this Activate.ps1 is intended to be run by Microsoft PowerShell. We must check which activate version to use if we’re running a different shell. The activate.bat file should be executed for cmd.
We are now inside our virtual environment using Python 3.10. To confirm, we can look at the left of our command prompt, which should display eda_venv.
In order to start using the new environment in our IDE, there’s one additional step we must perform; this heavily depends on which IDE we’re using, but typically we’ll have to point it to our new interpreter (eda_venv/Scripts/python.exe) by specifying its path on our preferences menu.
- On Spyder:
- We can head to Tools, Preferences, Python Interpreter.
- We can then input the interpreter’s path.
- On VS Code:
- We can open the command palette by pressing F1.
- We can then search for Python: Select Interpreter.
- We can input our interpreter’s path.
We can manage the required dependencies for our project by using arequirements.txt file. If we’re using a version control system such as GitHub, the best practice is to add our eda_venv folder to our .gitignore file. For this, we will create a new requirements.txt file and place it in our folder project:
Code
cd exporatory-data-analysis
New-Item requirements.txtWe will then include the following and save it:
Code
matplotlib
seaborn
numpy
pandas
scipy
scikit-learn
keras
xgboost
tensorflow==2.10
xlsxwriter
visualkeras
pydot
pydotplusIf we’re using a Windows machine, we can install tensorflow r2.10 since this was the last release to support GPU processing on native Windows. We can also stick with the tensorflow-cpu package since our data set is not extensive, but tensorflow leverages GPU processing power to perform faster, especially in deep learning models. We will use the GPU-powered tensorflow package for this segment, hence the version definition on our requirements.txt file.
We will also need to install the NVIDIA CUDA Toolkit & the CUDA Deep Neural Network (cuDNN) library if we wish to enable GPU processing. We can head to the CUDA Toolkit Downloads page and get the version for our case (it’s important to read all CUDA requirements, i.e. Visual Studio is required for it to work properly. Also, tensorflow requires a specific CUDA version). For cuDNN, we can head to the NVIDIA cuDNN page (we will have to create an NVIDIA developer account for this one).
3. Preparing our environment
Now that we have our environment ready, we can install all our packages using the requirements.txt file we just generated:
Code
cd exploratory-data-analysis
pip install -r requirements.txtAnd that’s it; we have every package we need on our virtual environment and ready to be imported.
We can then import the required modules:
Code
# Data manipulation modules
import pandas as pd
import numpy as np
import xlsxwriter
import re
# Plotting modules
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sn
from sklearn import tree
import visualkeras
from PIL import ImageFont
# Preprocessing modules
from sklearn.preprocessing import LabelEncoder, StandardScaler, FunctionTransformer
from sklearn.model_selection import train_test_split, KFold
# Evaluation & performance modules
from sklearn.metrics import confusion_matrix, classification_report
# Machine Learning models
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB, BernoulliNB
from sklearn.linear_model import SGDClassifier
from sklearn.ensemble import GradientBoostingClassifier
from xgboost import XGBClassifier
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
# Utility modules
import warnings
import shutilWe can suppress unnecessary warnings and define plot parameters:
Code
# Supress verbose warnings
warnings.filterwarnings("ignore")
# Define plot parameters
# Before anything else, delete the Matplotlib
# font cache directory if it exists, to ensure
# custom font propper loading
try:
shutil.rmtree(matplotlib.get_cachedir())
except FileNotFoundError:
pass
# Define main color as hex
color_main = '#1a1a1a'
# Define title & label padding
text_padding = 18
# Define font sizes
title_font_size = 17
label_font_size = 14
# Define rc params
plt.rcParams['figure.figsize'] = [14.0, 7.0]
plt.rcParams['figure.dpi'] = 300
plt.rcParams['grid.color'] = 'k'
plt.rcParams['grid.linestyle'] = ':'
plt.rcParams['grid.linewidth'] = 0.5
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['Lora']As we have multiple models, it will be best to build a dictionary with each name as Key and each model as Value. We will also define our model parameters inside each model so we don’t have to define them as additional variables in our workspace:
Code
# Define model dictionary
model_dictionary = {
'Multinomial Logistic Regressor': LogisticRegression(multi_class='multinomial',
solver='lbfgs',
random_state=42,
max_iter=100000,
penalty='l2',
C=24),
'Logistic Regressor' : LogisticRegression(C=24),
'Decision Tree Classifier': DecisionTreeClassifier(random_state=9),
'Random Forest Classifier': RandomForestClassifier(n_estimators = 100),
'Support Vector Classifier': SVC(C=0.12, gamma=0.02, kernel='linear'),
'Support Vector Classifier Polynomial Kernel': SVC(C=1, gamma=0.6, kernel='poly', degree=8),
'Support Vector Classifier Radial Kernel': SVC(C=1, gamma=0.6, kernel='rbf'),
'K-Nearest Neighbors Classifier' : KNeighborsClassifier(n_neighbors=5),
'Gaussian Naive Bayes Classifier': GaussianNB(),
'Bernoulli Naive Bayes Classifier': BernoulliNB(),
'Stochastic Gradient Descent': SGDClassifier(loss='log',
max_iter=10000,
random_state=42,
penalty='l2'),
'Gradient Boosting Classifier': GradientBoostingClassifier(),
'Extreme Gradient Boosting Classifier' : XGBClassifier(),
'Sequential Deep Neural Network' : Sequential()
}We can then define a dictionary which will contain all the preprocessing functions that we will need:
Code
preprocessing_dictionary = {'Right Skew Gaussian' : FunctionTransformer(func = np.square),
'Left Skew Gaussian' : FunctionTransformer(func = np.log1p),
'Standard Scaler' : StandardScaler()
}We can then import our data set and do some preprocessing:
Code
# Read the data set
df = pd.read_csv('cancer patient data sets.csv')
# Remove index column
df.drop(columns = "index", inplace = True)
# Map Level to numeric values
illness_level_dict = {'Low' : 1,
'Medium' : 2,
'High': 3}
df['Level'] = df['Level'].map(illness_level_dict)
# Remove columns that we will not study
remove_cols = ['Patient Id',
'Gender',
'Age',
'Chest Pain',
'Coughing of Blood',
'Fatigue',
'Weight Loss',
'Shortness of Breath',
'Wheezing',
'Swallowing Difficulty',
'Clubbing of Finger Nails',
'Frequent Cold',
'Dry Cough',
'Snoring']
df = df.drop(columns = remove_cols)
print(df.shape)
print(list(df.columns))We end up with a DataFrame with the following characteristics:
Output
(1000, 26)
['Air Pollution', 'Alcohol use', 'Dust Allergy', 'OccuPational Hazards', 'Genetic Risk', 'chronic Lung Disease', 'Balanced Diet', 'Obesity', 'Smoking', 'Passive Smoker', 'Level']If we recall from the last section, these are the potential risk factors that our client is looking to study. We had to remove all the other symptomatic characteristics as our client is not interested in these.
We will now define a simple function that will help us split our data into train and test sets:
Code
def sep(dataframe):
'''
Parameters
----------
dataframe : DataFrame
Contains our data as a DataFrame object.
Returns
-------
x : DataFrame
Contains our features.
y : DataFrame
Contains our labels.
'''
target = ["Level"]
x = dataframe.drop(target , axis = 1)
y = dataframe[target]
return x, yWe will now define three functions that will help us with the results generation:
cm_plotwill plot a confusion matrix for each method. Confusion matrices are a special kind of contingency table with two dimensions (actual and predicted). The idea behind the confusion matrix is to get a quick graphical grasp of how our model performed in predicting compared to the test data. It is a widely used and straightforward method to implement and explain to a non-technical audience.model_scorewill calculate the model score as the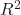 coefficient.
coefficient.classification_repwill calculate ,
, 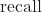 ,
,  and
and  for each label and return it as a DataFrame object.
for each label and return it as a DataFrame object.
Code
# Define Confusion Matrix Function
def cm_plot(model_name, model, test_y, predicted_y):
'''
Parameters
----------
model_name : Str
Contains the used model name.
model : sklearn or keras model object
Contains a model object depending on the model used.
test_y : DataFrame
Contains the non-scaled test values for our data set.
predicted_y : Array
Contains the predicted values for a given method.
Returns
-------
None.
'''
cm = confusion_matrix(test_y, predicted_y)
plt.figure(f'{model_name}_confusion_matrix')
sn.heatmap(cm, annot=True, linewidth=0.7, cmap="rocket")
plt.title(f'{model_name} Confusion Matrix\n')
plt.xlabel('y Predicted')
plt.ylabel('y Test')
plt.savefig('plots/' + f'{model_name}_confusion_matrix_tp.png', format = 'png', dpi = 300, transparent = True)
plt.close()
return None
# Define model score
def model_score(model, test_x, test_y):
'''
Parameters
----------
model : sklearn or keras model object
Contains a model object depending on the model used.
test_x : Array
Contains the transformed / scaled test values for the features.
test_y : DataFrame
Contains the un-scaled / un-transformed test values for the labels.
Returns
-------
sc : Float
Contains the score model.
'''
sc = model.score(test_x, test_y)
return sc
# Define Classification Report Function
def classification_rep(test_y, predicted_y):
'''
Parameters
----------
test_y : DataFrame
Contains the non-scaled test values for our data set.
predicted_y : Array
Contains the predicted values for a given method.
Returns
-------
cr : DataFrame
Contains a report showing the main classification metrics.
'''
cr = classification_report(test_y, predicted_y, output_dict=True)
cr = pd.DataFrame(cr).transpose()
return crWe will now transform our data in order to make it usable for each model:
Code
# For Normal Distribution Methods, we can approximate our data set to
# a normal distribution
right_skew = []
left_skew = []
for i in df_x.columns:
if df_x[i].skew() > 0:
right_skew.append(i)
else:
left_skew.append(i)
right_skew_transformed = preprocessing_dictionary['Right Skew Gaussian'].fit_transform(df_x[right_skew])
left_skew_transformed = preprocessing_dictionary['Left Skew Gaussian'].fit_transform(df_x[left_skew])
df_gaussian = pd.concat([right_skew_transformed,
left_skew_transformed ,
df_y] ,
axis = 1,
join = "inner")
# We can divide into train & text, x & y
train_G, test_G = train_test_split(df_gaussian, test_size=0.2)
train_Gx, train_Gy = sep(train_G)
test_Gx, test_Gy = sep(test_G)
# For other methods, we can scale using Standard Scaler
train, test = train_test_split(df, test_size=0.2)
train_x, train_Sy = sep(train)
test_x, test_Sy = sep(test)
train_Sx = preprocessing_dictionary['Standard Scaler'].fit_transform(train_x)
test_Sx = preprocessing_dictionary['Standard Scaler'].transform(test_x)Now that we have our transformed sets, we can start talking about the selected models. For each case, we will briefly describe what the model is about, its general mathematical intuition, and its assumptions.
The mathematical background provided in this segment is, by any means, a rigorous derivation. We could spend an entire series talking about one model’s mathematical background. Instead, we will review the main mathematical formulae involved in each model.
4. A word on model assumptions
Assumptions denote the collection of explicitly stated (or implicit premised) conventions, choices and other specifications on which any model is based.
Every model is built on top of assumptions. They provide the theoretical foundation for it to exist and be valid, and machine learning models are no exception. That is not to say that every assumption must be rigorously met for a given model to work as expected, but we cannot bypass every assumption and expect our model to work as designed.
If we understand the underlying theory behind our model, we can be selective in the assumptions we can live without; we can gain knowledge on the implications of bypassing a particular assumption and thus make a supported decision on which model to use. It’s a matter of balance and finding out what’s suitable for our case.
5. Multinomial Logistic Regression
Multinomial Logistic Regression is a classification method that generalizes logistic regression to multiclass problems, i.e. when we have more than two possible discrete outcomes.
Logistic Regression, or Logit Model, contrary to what its name may suggest, is not a regression model but a parametric classification one. In reality, this model is very similar to Linear Regression; the main difference between the two is that in Logistic Regression, we don’t fit a straight line to our data. Instead, we fit an ![]() shaped curve, called Sigmoid, to our observations.
shaped curve, called Sigmoid, to our observations.
5.1 Mathematical intuition overview
Logistic Regression fits data to a ![]() function:
function:
![]()
It first calculates a weighted sum of inputs:
![]()
It then calculates the probability of the weighted feature belonging to a given group:
![]()
Weights are calculated using different optimization models, such as Gradient Descent or Maximum Likelihood.
Multinomial Logistic Regression uses a linear predictor function ![]() to predict the probability that observation
to predict the probability that observation ![]() has outcome
has outcome ![]() , of the following form:
, of the following form:
![]()
Where:
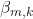 is the set of regression coefficients.
is the set of regression coefficients.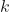 is the outcome.
is the outcome. is a row vector containing the set of explanatory variables associated with observation
is a row vector containing the set of explanatory variables associated with observation 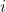 .
.
We can express our predictor function in a more compact form, since the regression coefficients and explanatory variables are normally grouped into vectors of size ![]() :
:
![]()
When fitting a multinomial logistic regression model, we have several outcomes (![]() ), meaning we can think of the problem as fitting
), meaning we can think of the problem as fitting ![]() independent Binary Logit Models. From the Binary Logit Model equation, we can express our predictor functions as follows:
independent Binary Logit Models. From the Binary Logit Model equation, we can express our predictor functions as follows:
![]()
![]()
![]()
![]()
We can then exponentiate both sides of our equation to get probabilities:
![]()
![]()
![]()
![]()
5.2 Assumptions
- It requires the dependent variable to be binary, multinomial or ordinal.
- It has a linear decision surface, meaning it can’t solve non-linear problems.
- Requires very little to no multicollinearity, meaning our independent variables must not be correlated with each other.
- Usually works best with large data sets and requires sufficient training examples for all the categories to make correct predictions.
5.3 Implementation
We can start by fitting our model to our data:
Code
# Train model
model_dictionary['Multinomial Logistic Regressor'].fit(train_Sx, train_Sy)We can then predict some values using our trained model:
Code
# Predict
y_predicted_MLogReg = model_dictionary['Multinomial Logistic Regressor'].predict(test_Sx)We can finally evaluate our model using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
cm_plot('Multinomial Logistic Regressor',
model_dictionary['Multinomial Logistic Regressor'],
test_Sy,
y_predicted_MLogReg)
# Define model score
score_MLogReg = model_score(model_dictionary['Multinomial Logistic Regressor'],
test_Sx,
test_Sy)
# Define Classification Report Function
report_MLogReg = classification_rep(test_Sy,
y_predicted_MLogReg)
print(score_MLogReg)Output
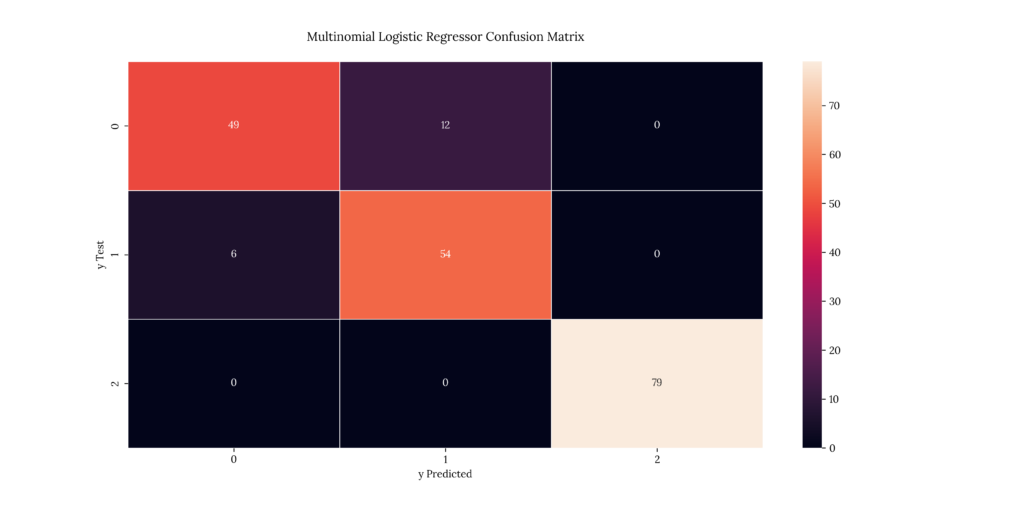
As we discussed earlier, a confusion matrix tells us the number of predicted values for each severity level vs the test values we’re comparing results with. The matrix diagonal denotes the predicted & test value match.
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 0.890909 | 0.803279 | 0.844828 | 61 |
| 2 | 0.818182 | 0.9 | 0.857143 | 60 |
| 3 | 1 | 1 | 1 | 79 |
| accuracy | 0.91 | 0.91 | 0.91 | 0.91 |
| macro avg | 0.90303 | 0.901093 | 0.900657 | 200 |
| weighted avg | 0.912182 | 0.91 | 0.909815 | 200 |
A classification report has 7 different metrics:
The precision is the number of true positive results divided by the number of all positive results, including those not identified correctly:
![]()
Where:
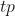 are the true positives.
are the true positives.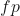 are the false positives.
are the false positives.
The recall is the number of true positive results divided by the number of all samples that should have been identified as positive:
![]()
Where:
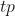 are the true positives.
are the true positives.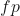 are the false positives.
are the false positives.
The f1-score is the harmonic mean of the precision and recall. The highest possible value of an F-score is 1.0, indicating perfect precision and recall, and the lowest possible value is 0 if either precision or recall is zero:
![]()
The accuracy is the sum of true positives and true negatives divided by the total number of samples. This is only accurate if the model is balanced. It will give inaccurate results if there is a class imbalance:
![]()
Where:
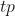 are the true positives.
are the true positives. are the true negatives.
are the true negatives.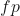 are the false positives.
are the false positives. are the false negatives.
are the false negatives.
In our case, we have a balanced class. We can confirm this fact:
Code
df.groupby('Level')['Level'].count() / len(df) * 100Output
Level
1 30.3
2 33.2
3 36.5
Name: Level, dtype: float64We can see that we have roughly the same percentage of patients distributed along Lung Cancer severity levels, so for our case, the accuracy metric will be the most helpful way to evaluate our models.
If we had an unbalanced label class, we would have to perform special treatments to implement our models, and we would not be able to use accuracy as our model evaluator.
The macro-averaged f1-score is computed using the arithmetic or unweighted mean of all the per-class f1 scores.
The weighted average of precision, recall and f1-score takes the weights as the support values.
If we take a look at our results, we can see that it predicted with a 91.5% accuracy:
Output
0.915Not to worry, we will explore the results in more detail in the Method Comparison section.
We can now use a Binomial Logistic Regression model and see what we get:
Code
# Train model
model_dictionary['Logistic Regressor'].fit(train_Sx, train_Sy)
# Predict
y_predicted_BLogReg = model_dictionary['Logistic Regressor'].predict(test_Sx)
# Evaluate the model and collect the scores
cm_plot('Logistic Regressor',
model_dictionary['Logistic Regressor'],
test_Sy,
y_predicted_BLogReg)
# Define model score
score_BLogReg = model_score(model_dictionary['Logistic Regressor'],
test_Sx,
test_Sy)
# Define Classification Report Function
report_BLogReg = classification_rep(test_Sy,
y_predicted_BLogReg)
print(score_BLogReg)If we look at our results, we can see that it predicted with a 91.5% accuracy. Same as its multinomial cousin:
Output
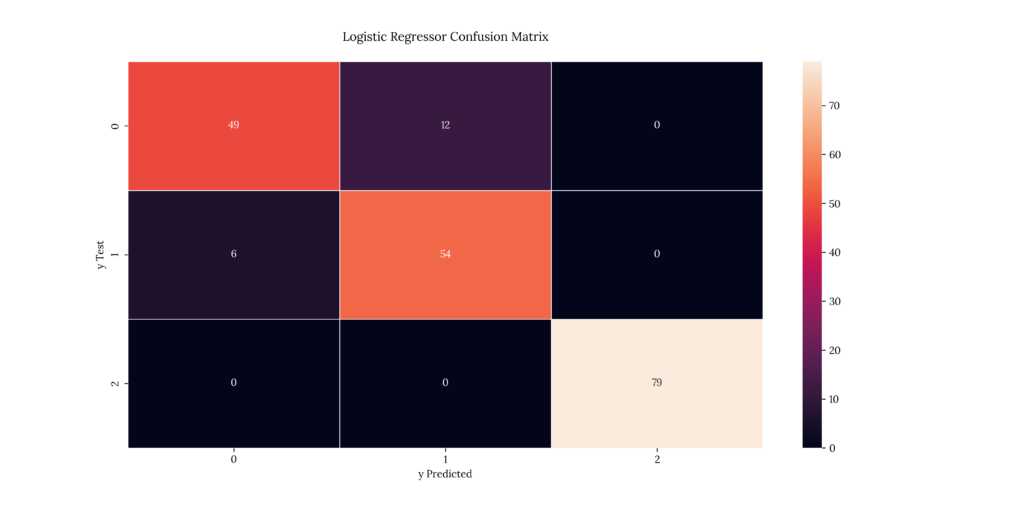
Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 0.890909 | 0.803279 | 0.844828 | 61 |
| 2 | 0.818182 | 0.9 | 0.857143 | 60 |
| 3 | 1 | 1 | 1 | 79 |
| accuracy | 0.91 | 0.91 | 0.91 | 0.91 |
| macro avg | 0.90303 | 0.901093 | 0.900657 | 200 |
| weighted avg | 0.912182 | 0.91 | 0.909815 | 200 |
Output
0.9156. Decision Tree
A Decision Tree is a technique that can be used for classification and regression problems. In our case, we’ll be using a Decision Tree Classifier.
A Decision Tree has two types of nodes:
- Decision Node: These are in charge of making decisions and branch in multiple nodes.
- Leaf Node: These are the outputs of the decision nodes and do not branch further.
A Decision Tree algorithm starts from the tree’s root node containing the entire data set. It then divides the root node into subsets containing possible values for the best attributes. It then compares values of the best attribute using Attribute Selection Measures (ASM). It then generates a new node, which includes the best attribute. Finally, it recursively makes new decision trees using the subsets of the dataset and continues until a stage is reached where it cannot further classify the nodes. This is where the final node (leaf node) is created.
6.1 Mathematical intuition overview
Attribute Selection Measures (ASM) determine which attribute to select as a decision node and branch further. There are two main ASMs:
6.1.1 Information Gain
Measures the change in entropy after the segmentation of a dataset based on an attribute occurs:
![]()
We can interpret entropy as impurity in a given attribute:
![]()
Where:
 is the data set
is the data set  .
. is the dataset
is the dataset  .
. represents the proportion of the values in
represents the proportion of the values in  to the number of values in dataset,
to the number of values in dataset,  .
.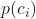 is the probability of class
is the probability of class 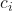 in a node.
in a node.
The more entropy removed, the greater the information gain. The higher the information gain, the better the split.
6.1.2 Gini Index
Measures impurity; if all the elements belong to a single class, it can be called pure. The degree of the Gini Index varies between 0 and 1. A Gini Index of 0 denotes that all elements belong to a certain class or only one class exists (pure). A Gini Index of 1 denotes that the elements are randomly distributed across various classes (impure).
Gini Index is expressed with the following equation:
![]()
Where:
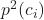 is the squared probability of class
is the squared probability of class 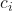 in a node.
in a node.
6.2 Assumptions
- In the beginning, the whole training set is considered the root.
- Feature values are preferred to be categorical.
- Records are distributed recursively based on attribute values.
6.3 Implementation
We can start by fitting our model to our data:
Code
# Train model
model_dictionary['Decision Tree Classifier'].fit(train_Sx, train_Sy)We can then predict some values using our trained model:
Code
# Predict
y_predicted_DecTree = model_dictionary['Decision Tree Classifier'].predict(test_Sx)We can finally evaluate our model using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
cm_plot('Decision Tree Classifier',
model_dictionary['Decision Tree Classifier'],
test_Sy,
y_predicted_DecTree)
# Define model score
score_DecTree = model_score(model_dictionary['Decision Tree Classifier'],
test_Sx,
test_Sy)
# Define Classification Report Function
report_DecTree = classification_rep(test_Sy,
y_predicted_DecTree)
print(score_DecTree)If we take a look at our results, we can see that it predicted with a 100% accuracy:
Output
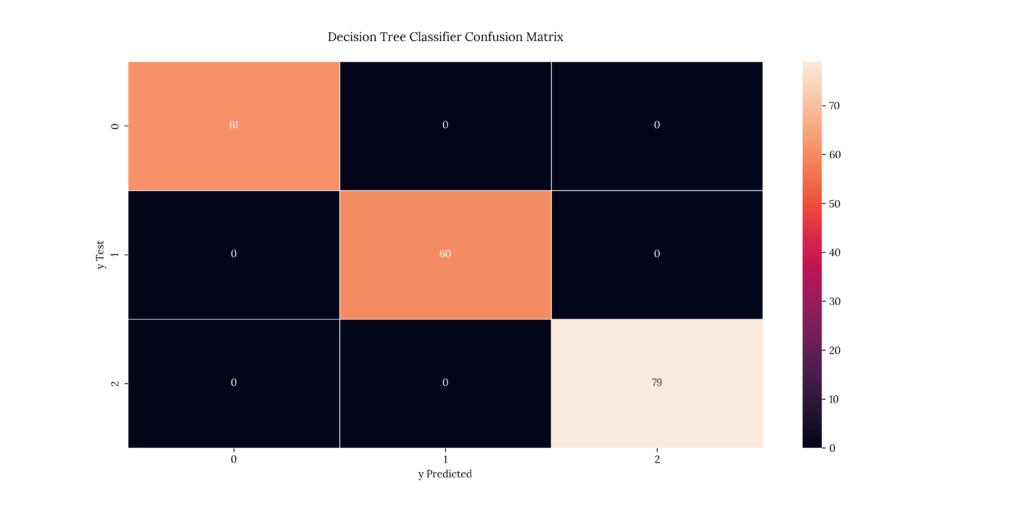
Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 61 |
| 2 | 1 | 1 | 1 | 60 |
| 3 | 1 | 1 | 1 | 79 |
| accuracy | 1 | 1 | 1 | 1 |
| macro avg | 1 | 1 | 1 | 200 |
| weighted avg | 1 | 1 | 1 | 200 |
Output
1.0The interesting thing about Decision Trees is that we can visualize them using multiple methods.
We can display a simple text representation:
Code
# Text Representation
DecTree_text_rep = tree.export_text(model_dictionary['Decision Tree Classifier'])
print(DecTree_text_rep)Output
|--- feature_7 <= 0.99
| |--- feature_2 <= -1.29
| | |--- feature_6 <= 0.50
| | | |--- class: 1
| | |--- feature_6 > 0.50
| | | |--- class: 3
| |--- feature_2 > -1.29
| | |--- feature_9 <= 1.03
| | | |--- feature_1 <= -0.00
| | | | |--- feature_7 <= -0.89
| | | | | |--- feature_1 <= -1.16
| | | | | | |--- feature_3 <= -0.63
| | | | | | | |--- class: 2
| | | | | | |--- feature_3 > -0.63
| | | | | | | |--- class: 1
| | | | | |--- feature_1 > -1.16
| | | | | | |--- class: 1
| | | | |--- feature_7 > -0.89
| | | | | |--- feature_6 <= -0.42
| | | | | | |--- feature_1 <= -0.77
| | | | | | | |--- feature_0 <= -0.14
| | | | | | | | |--- feature_1 <= -1.16
| | | | | | | | | |--- feature_7 <= -0.42
| | | | | | | | | | |--- class: 1
| | | | | | | | | |--- feature_7 > -0.42
| | | | | | | | | | |--- class: 2
| | | | | | | | |--- feature_1 > -1.16
| | | | | | | | | |--- class: 2
| | | | | | | |--- feature_0 > -0.14
| | | | | | | | |--- class: 1
| | | | | | |--- feature_1 > -0.77
| | | | | | | |--- feature_6 <= -0.89
| | | | | | | | |--- class: 1
| | | | | | | |--- feature_6 > -0.89
| | | | | | | | |--- class: 2
| | | | | |--- feature_6 > -0.42
| | | | | | |--- feature_7 <= 0.28
| | | | | | | |--- class: 1
| | | | | | |--- feature_7 > 0.28
| | | | | | | |--- class: 2
| | | |--- feature_1 > -0.00
| | | | |--- feature_5 <= 1.17
| | | | | |--- class: 2
| | | | |--- feature_5 > 1.17
| | | | | |--- class: 1
| | |--- feature_9 > 1.03
| | | |--- class: 3
|--- feature_7 > 0.99
| |--- feature_0 <= -0.63
| | |--- class: 2
| |--- feature_0 > -0.63
| | |--- class: 3We can also plot the tree using plot_tree:
Code
# Tree plot using plot_tree
fig = plt.figure('Decision Tree plot_tree')
tree.plot_tree(model_dictionary['Decision Tree Classifier'],
feature_names=df_x.columns,
class_names=df_y['Level'].astype('str'),
filled=True)
plt.title('Decision Tree Plot')
plt.savefig('plots/' + 'Decision Tree Classifier_Decision Tree_tp.png', format = 'png', dpi = 300, transparent = True)
plt.close()Output
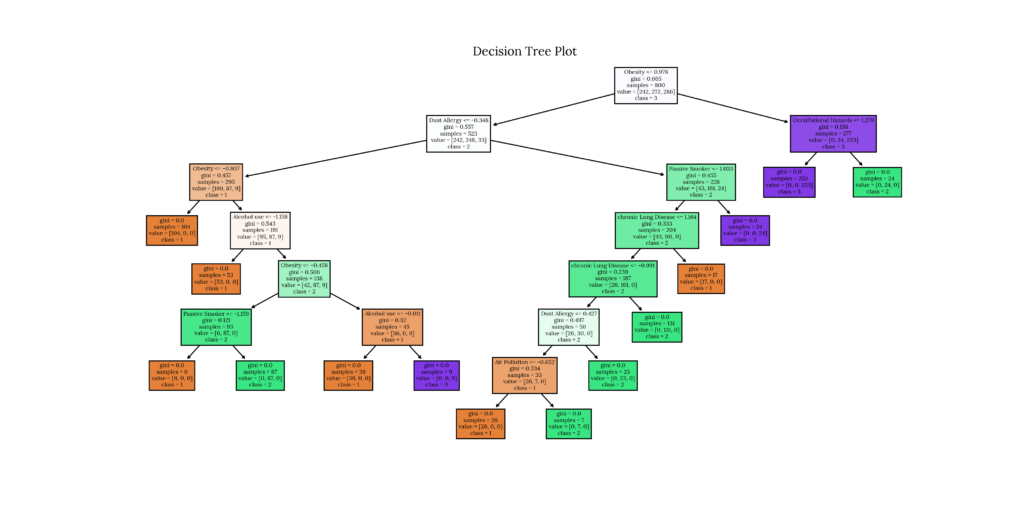
7. Random Forest
Random Forest is an ensemble learning method for classification, regression and other methods. It works by constructing a multitude of decision trees at training time; the output of the random forest is the class selected by most trees.
7.1 Mathematical intuition overview
Given a training set ![]() with responses
with responses ![]() bagging repeatedly (B times) selects a random sample with replacement of the training set and fits trees to these samples.
bagging repeatedly (B times) selects a random sample with replacement of the training set and fits trees to these samples.
After training, predictions for unseen samples ![]() can be made by averaging the predictions from all the individual regression trees on
can be made by averaging the predictions from all the individual regression trees on ![]() or by taking the majority vote from the set of trees.
or by taking the majority vote from the set of trees.
We can also include a measure of the uncertainty of the prediction calculating the standard deviation of the predictions from all the individual regression trees on ![]() .
.
7.2 Assumptions
- It inherits assumptions from the decision tree model.
- There should be some actual values in the feature variables of the dataset, which will give the classifier a better chance to predict accurate results.
- The predictions from each tree must have very low correlations.
7.3 Implementation
We can start by fitting our model to our data:
Code
# Train model
model_dictionary['Random Forest Classifier'].fit(train_Sx, train_Sy)We can then predict some values using our trained model:
Code
# Predict
y_predicted_RandomFor = model_dictionary['Random Forest Classifier'].predict(test_Sx)We can finally evaluate our model using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
cm_plot('Random Forest Classifier',
model_dictionary['Random Forest Classifier'],
test_Sy,
y_predicted_RandomFor)
# Define model score
score_RandomFor = model_score(model_dictionary['Random Forest Classifier'],
test_Sx,
test_Sy)
# Define Classification Report Function
report_RandomFor = classification_rep(test_Sy,
y_predicted_RandomFor)
print(score_RandomFor)If we take a look at our results, we can see that it predicted with a 100% accuracy:
Output
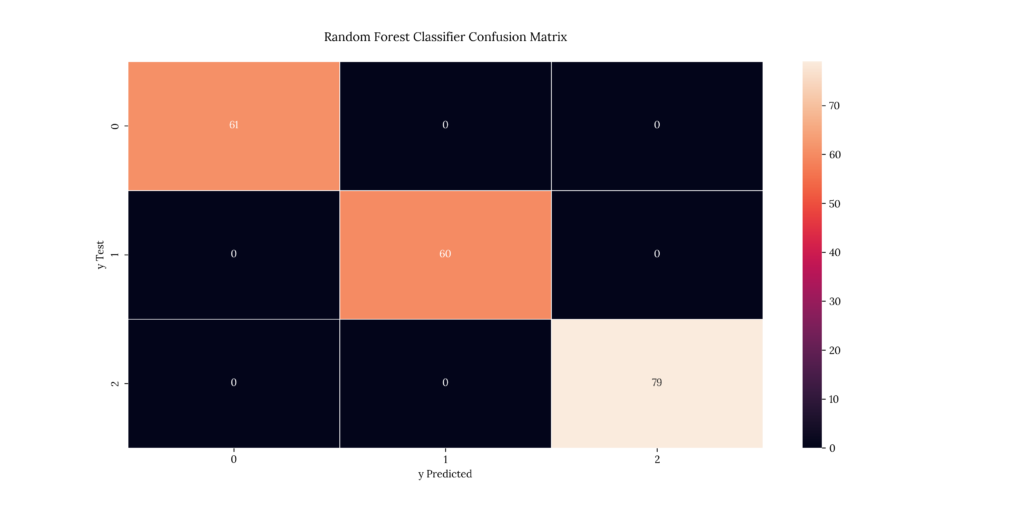
Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 61 |
| 2 | 1 | 1 | 1 | 60 |
| 3 | 1 | 1 | 1 | 79 |
| accuracy | 1 | 1 | 1 | 1 |
| macro avg | 1 | 1 | 1 | 200 |
| weighted avg | 1 | 1 | 1 | 200 |
Output
1.08. Nonlinear Support Vector Machine
Support Vector Machines (SVM) are a class of supervised models originally developed for linear applications, although a nonlinear implementation using nonlinear Kernels was also developed; the resulting algorithm is similar, except that every dot product is replaced by a nonlinear kernel function.
8.1 Mathematical intuition overview
The SVM model amounts to minimizing an expression of the following form:
![]()
Where:
 is the loss function.
is the loss function. is the regularization.
is the regularization.
With the different nonlinear Kernels being:
- Polynomial homogeneous (when
 , this becomes the linear kernel):
, this becomes the linear kernel): 
- Polynomial homogeneous:

- Gaussian Radial Basis Function (RBF):
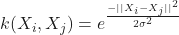 , for
, for 
- Sigmoid function:
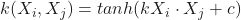 , for some
, for some  and
and 
8.2 Assumptions
There are no particular assumptions for this model. If we scale our variables, we might increase its performance, but it is not required.
8.3 Implementation
For this part, we’ll be using three different approaches; we mentioned that Support Vector Machines are fit for linear applications, although we can use nonlinear Kernels to fit nonlinear data.
There are two particular Kernels we will implement:
- Polynomial Kernel: As its name suggests, this Kernel represents the similarity of vectors in a feature space over polynomials of the original variables. We can select the order of the polynomial as a parameter.
- Radial Basis Function Kernel: This Kernel is the most generalized form of kernelization and is one of the most widely used in SVM due to its similarity to the Gaussian distribution.
We can start by fitting our models to our data:
Code
# Train models
model_dictionary['Support Vector Classifier'].fit(train_Sx, train_Sy)
model_dictionary['Support Vector Classifier Polynomial Kernel'].fit(train_Sx, train_Sy)
model_dictionary['Support Vector Classifier Radial Kernel'].fit(train_Sx, train_Sy)We can then predict some values using our trained models:
Code
# Predict
y_predicted_SVM = model_dictionary['Support Vector Classifier'].predict(test_Sx)
y_predicted_SVMp = model_dictionary['Support Vector Classifier Polynomial Kernel'].predict(test_Sx)
y_predicted_SVMr = model_dictionary['Support Vector Classifier Radial Kernel'].predict(test_Sx)We can finally evaluate our models using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
cm_plot('Support Vector Classifier',
model_dictionary['Support Vector Classifier'],
test_Sy,
y_predicted_SVM)
cm_plot('Support Vector Classifier Polynomial Kernel',
model_dictionary['Support Vector Classifier Polynomial Kernel'],
test_Sy,
y_predicted_SVMp)
cm_plot('Support Vector Classifier Radial Kernel',
model_dictionary['Support Vector Classifier Radial Kernel'],
test_Sy,
y_predicted_SVMr)
# Define model score
score_SVM = model_score(model_dictionary['Support Vector Classifier'],
test_Sx,
test_Sy)
score_SVMp = model_score(model_dictionary['Support Vector Classifier Polynomial Kernel'], test_Sx, test_Sy)
score_SVMr = model_score(model_dictionary['Support Vector Classifier Radial Kernel'], test_Sx, test_Sy)
# Define Classification Report Function
report_SVM = classification_rep(test_Sy,
y_predicted_SVM)
report_SVMp = classification_rep(test_Sy,
y_predicted_SVMp)
report_SVMr = classification_rep(test_Sy,
y_predicted_SVMr)
print(score_SVM)
print(score_SVMp)
print(score_SVMr)If we look at our results, we can see that we get the following accuracies:
- Linear SVM: 88.5%
- Polynomial SVM, 8th degree: 100%
- Radial Kernel: 100%
Output

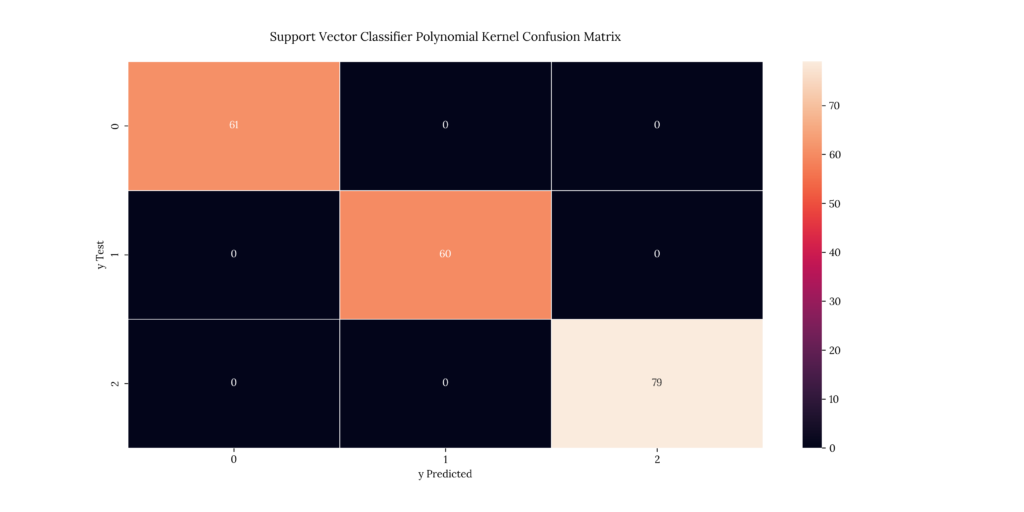
Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 0.780822 | 0.934426 | 0.850746 | 61 |
| 2 | 0.888889 | 0.666667 | 0.761905 | 60 |
| 3 | 0.95122 | 0.987342 | 0.968944 | 79 |
| accuracy | 0.875 | 0.875 | 0.875 | 0.875 |
| macro avg | 0.873643 | 0.862812 | 0.860532 | 200 |
| weighted avg | 0.880549 | 0.875 | 0.870782 | 200 |
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 61 |
| 2 | 1 | 1 | 1 | 60 |
| 3 | 1 | 1 | 1 | 79 |
| accuracy | 1 | 1 | 1 | 1 |
| macro avg | 1 | 1 | 1 | 200 |
| weighted avg | 1 | 1 | 1 | 200 |
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 61 |
| 2 | 1 | 1 | 1 | 60 |
| 3 | 1 | 1 | 1 | 79 |
| accuracy | 1 | 1 | 1 | 1 |
| macro avg | 1 | 1 | 1 | 200 |
| weighted avg | 1 | 1 | 1 | 200 |
Output
0.885
1.0
1.09. K-Nearest Neighbors
K-Nearest Neighbors (KNN) is a non-parametric, supervised learning classifier which uses proximity to classify and group data points. A class label is assigned based on a majority vote i.e. the label that is most frequently represented around a given data point is used. The KNN model chooses ![]() nearest points by calculating distances using different metrics and calculating an average to make a prediction.
nearest points by calculating distances using different metrics and calculating an average to make a prediction.
9.1 Mathematical intuition overview
Several distance metrics can be used:
9.1.1 Euclidean distance
This is the most one, and it is limited to real-valued vectors. It measures a straight line between two points: We can then predict some values using our trained models:
![]()
9.1.2 Manhattan distance
It is also referred to as taxicab distance or city block distance as it is commonly visualized using a grid:
![]()
9.1.3 Minkowski distance
This metric is the generalized form of Euclidean and Manhattan distance metrics. Euclidean distance takes ![]() , while Manhattan distance takes
, while Manhattan distance takes ![]()
![]()
9.1.4 Hamming distance
This technique is typically used with Boolean or string vectors. Interestingly, it’s also used in information theory as a way to measure the distance between two strings of equal length:
![]()
- If
 ,
,  ,
, - If
 ,
, 
9.2 Assumptions
- Items close together in the data set are typically similar
9.3 Implementation
We can start by fitting our model to our data:
Code
# Train model
model_dictionary['K-Nearest Neighbors Classifier'].fit(train_Sx, train_Sy)We can then predict some values using our trained model:
Code
# Predict
y_predicted_KNN = model_dictionary['K-Nearest Neighbors Classifier'].predict(test_Sx)We can finally evaluate our model using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
cm_plot('K-Nearest Neighbors Classifier',
model_dictionary['K-Nearest Neighbors Classifier'],
test_Sy,
y_predicted_KNN)
# Define model score
score_KNN = model_score(model_dictionary['K-Nearest Neighbors Classifier'],
test_Sx,
test_Sy)
# Define Classification Report Function
report_KNN = classification_rep(test_Sy,
y_predicted_KNN)
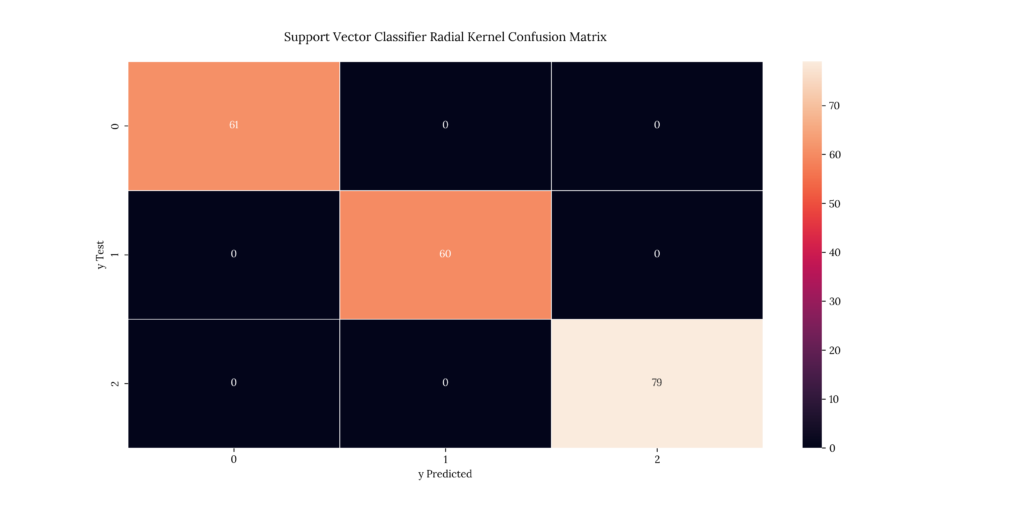
print(score_KNN)If we take a look at our results, we can see that it predicted with an 100% accuracy:
Output
Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 61 |
| 2 | 1 | 1 | 1 | 60 |
| 3 | 1 | 1 | 1 | 79 |
| accuracy | 1 | 1 | 1 | 1 |
| macro avg | 1 | 1 | 1 | 200 |
| weighted avg | 1 | 1 | 1 | 200 |
Output
1.011. Gaussian Naïve Bayes
Gaussian Naïve Bayes (GNB) is a probabilistic machine learning algorithm based on the Bayes’ Theorem. It is the extension of the Naïve Bayes algorithm, and as its name suggests, it approximates class-conditional distributions as a Gaussian distribution, with a mean ![]() and a standard deviation
and a standard deviation ![]() .
.
11.1 Mathematical intuition overview
We can start with the Bayes’ Theorem:
![]()
Where:
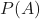 is the probability of
is the probability of 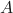 occurring.
occurring. is the probability of
is the probability of 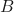 occurring.
occurring. is the probability of
is the probability of 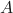 given
given 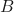 .
. is the probability of
is the probability of 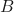 given
given 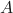 .
.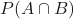 is the probability of
is the probability of 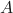 and
and 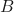 occurring.
occurring.
We can then translate the formula above to the Gaussian Naïve Bayes equation:
![]()
We can see that the form of this equation is almost identical to the Gaussian distribution density function. The main difference is that in the first one, we’re defining our function as a probability function, while in the latter, we’re defining it as a density function:
![]()
11.2 Assumptions
- Features are independent (hence Naïve).
- Class-conditional densities are normally distributed.
11.3 Implementation
Since we are using the Gaussian variant of the model, we will use the normally-approximated values we generated earlier. We can start by fitting our model to our data:
Code
# Train model
model_dictionary['Gaussian Naive Bayes Classifier'].fit(train_Gx, train_Gy)We can then predict some values using our trained model:
Code
# Predict
y_predicted_GNB = model_dictionary['Gaussian Naive Bayes Classifier'].predict(test_Gx)We can finally evaluate our model using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
cm_plot('Gaussian Naive Bayes Classifier',
model_dictionary['Gaussian Naive Bayes Classifier'],
test_Gy,
y_predicted_GNB)
# Define model score
score_GNB = model_score(model_dictionary['Gaussian Naive Bayes Classifier'],
test_Gx,
test_Gy)
# Define Classification Report Function
report_GNB = classification_rep(test_Gy,
y_predicted_GNB)
print(score_GNB)If we take a look at our results, we can see that it predicted with a 60.5% accuracy. This is the lowest score we’ve gotten so far:
Output
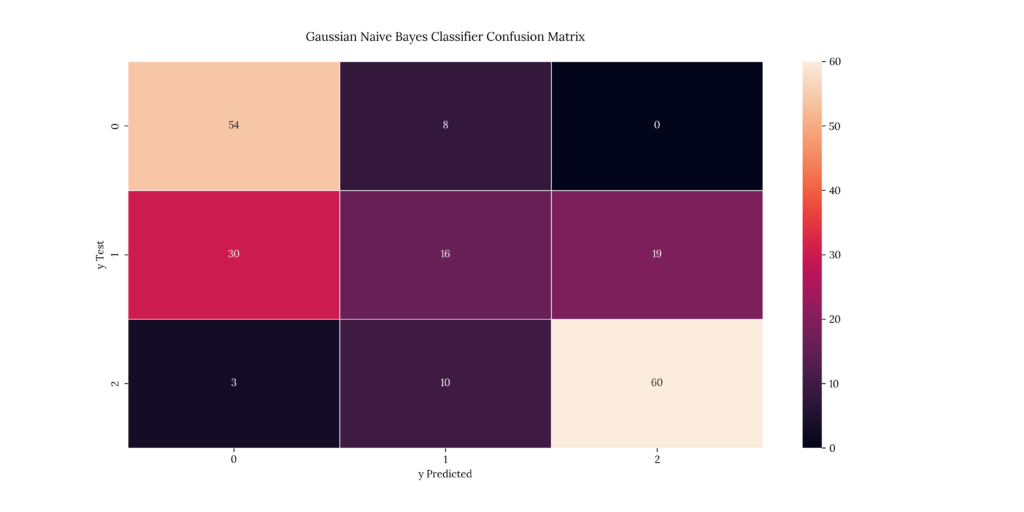
Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 0.62069 | 0.870968 | 0.724832 | 62 |
| 2 | 0.470588 | 0.246154 | 0.323232 | 65 |
| 3 | 0.759494 | 0.821918 | 0.789474 | 73 |
| accuracy | 0.65 | 0.65 | 0.65 | 0.65 |
| macro avg | 0.616924 | 0.646346 | 0.612513 | 200 |
| weighted avg | 0.62257 | 0.65 | 0.617906 | 200 |
Output
0.60512. Bernoulli Naïve Bayes
Bernoulli Naïve Bayes (BNB) is similar to Gaussian Naïve Bayes in that it also uses Bayes’ Theorem as its foundation. The difference is that Bernoulli Naïve Bayes approximates class-conditional distributions as a Bernoulli distribution. This fact makes this variation more appropriate for discrete random variables instead of continuous ones.
12.1 Mathematical intuition overview
Since we already went over Bayes’ Theorem, we can start by defining the Bernoulli distribution function:
![Rendered by QuickLaTeX.com p(x) =P[X=x] =\begin{cases}p & \text{if $x = 1$}, \\q=1 - p & \text{if $x = 0$}.\end{cases}](https://pabloagn.com/wp-content/ql-cache/quicklatex.com-c4cdd1e55d72e4f99e13d909ade8d0b3_l3.png)
From the above, we can then define the Bernoulli Naïve Bayes Classifier:
![]()
12.2 Assumptions
- The attributes are independent of each other and do not affect each other’s performance (hence Naïve).
- All of the features are given equal importance.
12.3 Implementation
We can start by fitting our model to our data:
Code
# Train model
model_dictionary['Bernoulli Naive Bayes Classifier'].fit(train_Sx, train_Sy)We can then predict some values using our trained model:
Code
# Predict
y_predicted_BNB = model_dictionary['Bernoulli Naive Bayes Classifier'].predict(test_Sx)We can finally evaluate our model using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
cm_plot('Bernoulli Naive Bayes Classifier',
model_dictionary['Bernoulli Naive Bayes Classifier'],
test_Sy,
y_predicted_BNB)
# Define model score
score_BNB = model_score(model_dictionary['Bernoulli Naive Bayes Classifier'],
test_Sx,
test_Sy)
# Define Classification Report Function
report_BNB = classification_rep(test_Sy,
y_predicted_BNB)
print(score_BNB)If we take a look at our results, we can see that it predicted with a 77.5% accuracy:
Output
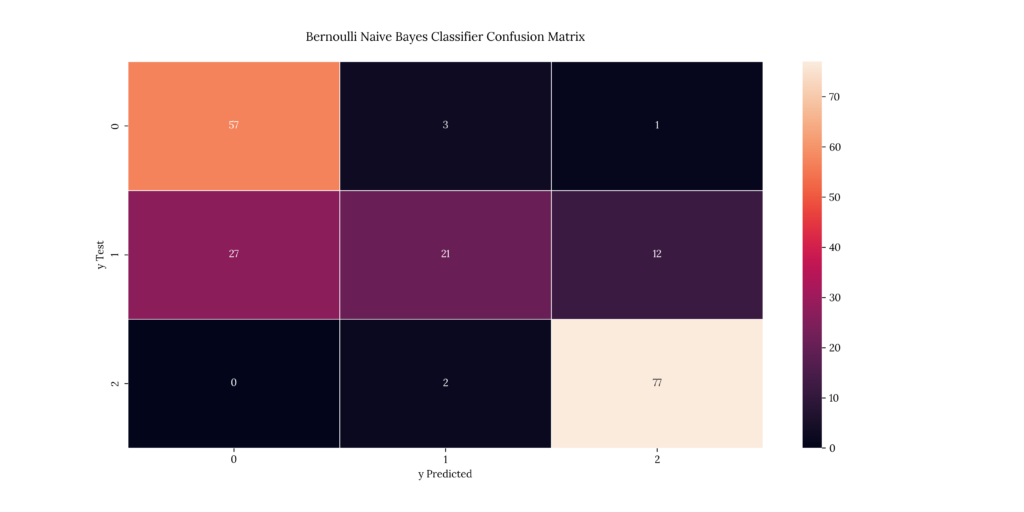
Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 0.678571 | 0.934426 | 0.786207 | 61 |
| 2 | 0.807692 | 0.35 | 0.488372 | 60 |
| 3 | 0.855556 | 0.974684 | 0.911243 | 79 |
| accuracy | 0.775 | 0.775 | 0.775 | 0.775 |
| macro avg | 0.780606 | 0.753037 | 0.728607 | 200 |
| weighted avg | 0.787216 | 0.775 | 0.746246 | 200 |
Output
0.77513. Stochastic Gradient Descent
Stochastic Gradient Descent (SGD) is an optimization method. It can be used in conjunction with other Machine Learning algorithms.
In general, gradient descent is used to minimize a cost function. There are three main types:
- Batch gradient descent
- Mini-batch gradient descent
- Stochastic gradient descent
Stochastic Gradient Descent computes the gradient by calculating the derivative of the loss of a single random data point rather than all of the data points (hence the name, stochastic). It then finds a minimum by taking steps. What makes it different from other optimization methods is its efficiency, i.e. it only uses one single random point to calculate the derivative.
The Stochastic Gradient Descent Classifier is a linear classification method with SGD training.
13.1 Mathematical intuition overview
The SGD gradient function can be expressed as follows:
![]()
Where:
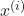 is a given training example.
is a given training example.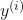 is a given label.
is a given label. is the true gradient of
is the true gradient of 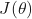
 is the approximation of the true gradient
is the approximation of the true gradient  at time
at time  by a gradient at a single sample.
by a gradient at a single sample.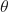 is the position of the previous step.
is the position of the previous step.
As the algorithm sweeps through the training set, it performs the above update for each training sample. Several passes can be made over the training set until the algorithm converges.
13.2 Assumptions
- The errors at each point in the parameter space are additive
- The expected value of the observation picked randomly is a subgradient of the function at point
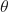 .
.
13.3 Implementation
For this example, we’ll use a Logistic Regressor with SGD training. We can start by fitting our model to our data:
Code
# Train model
model_dictionary['Stochastic Gradient Descent'].fit(train_Sx, train_Sy)We can then predict some values using our trained model:
Code
# Predict
y_predicted_SGD = model_dictionary['Stochastic Gradient Descent'].predict(test_Sx)We can finally evaluate our model using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
cm_plot('Stochastic Gradient Descent',
model_dictionary['Stochastic Gradient Descent'],
test_Sy,
y_predicted_SGD)
# Define model score
score_SGD = model_score(model_dictionary['Stochastic Gradient Descent'],
test_Sx,
test_Sy)
# Define Classification Report Function
report_SGD = classification_rep(test_Sy,
y_predicted_SGD)
print(score_SGD)If we take a look at our results, we can see that it predicted with an 80.5% accuracy:
Output
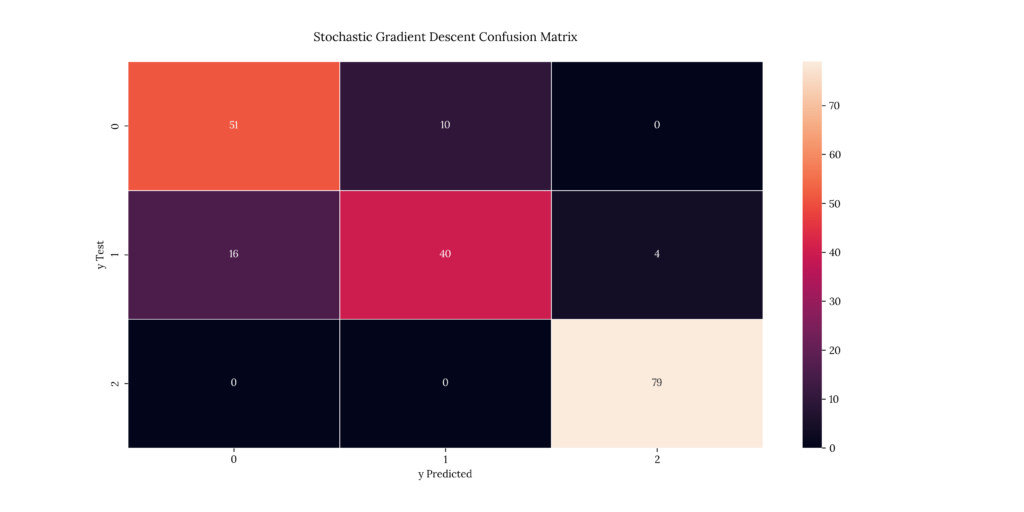
Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 0.761194 | 0.836066 | 0.796875 | 61 |
| 2 | 0.8 | 0.666667 | 0.727273 | 60 |
| 3 | 0.951807 | 1 | 0.975309 | 79 |
| accuracy | 0.85 | 0.85 | 0.85 | 0.85 |
| macro avg | 0.837667 | 0.834244 | 0.833152 | 200 |
| weighted avg | 0.848128 | 0.85 | 0.846476 | 200 |
Output
0.8514. Gradient Boosting
Gradient Boosting (GBM) is a machine learning technique used in regression and classification tasks to create a stronger model using an ensemble of weaker models. The objective of Gradient Boosting classifiers is to minimize the loss or the difference between the actual class value of the training example and the predicted class value. As with other classifiers, GBM depends on a loss function, which can be customized to improve performance.
Gradient Boosting Classifiers consist of three main parts:
- The weak model, usually a Decision Tree
- The additive component
- A loss function that is to be optimized
The main problem with Gradient Boosting is the potential of overfitting the model. We know that perfect training scores will lead to this phenomenon. This can be overcome by setting different regularization methods such as tree constraints, shrinkage and penalized learning.
14.1 Mathematical intuition overview
We can generalize a Gradient-Boosted Decision Tree model.
We can initialize our model with a constant loss function:
![]()
We can then compute the residuals:
![]()
We can then train our Decision Tree with features ![]() against
against ![]() and create terminal node regressions
and create terminal node regressions ![]() .
.
Next, we can compute a ![]() which minimizes our loss function on each terminal node:
which minimizes our loss function on each terminal node:
![]()
Finally, we can recompute the model with our new ![]() :
:
![]()
Where:
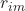 is the residual or gradient of our loss function.
is the residual or gradient of our loss function.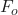 is our first iteration.
is our first iteration.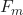 is the updated prediction.
is the updated prediction.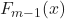 is the previous prediction.
is the previous prediction. is the learning rate between 0 and 1.
is the learning rate between 0 and 1. is the value which minimizes the loss function on each terminal node.
is the value which minimizes the loss function on each terminal node.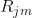 is the terminal node.
is the terminal node.
14.2 Assumptions
- The sum of its residuals is 0, i.e. the residuals should be spread randomly around zero.
14.3 Implementation
For this example, we’ll use a Gradient Boosting Classifier. We will leave parameters as default (100 estimators), although these can be fine-tuned. We can start by fitting our model to our data:
Code
# Train model
model_dictionary['Gradient Boosting Classifier'].fit(train_Sx, train_Sy)We can then predict some values using our trained model:
Code
# Predict
y_predicted_GBC = model_dictionary['Gradient Boosting Classifier'].predict(test_Sx)We can finally evaluate our model using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
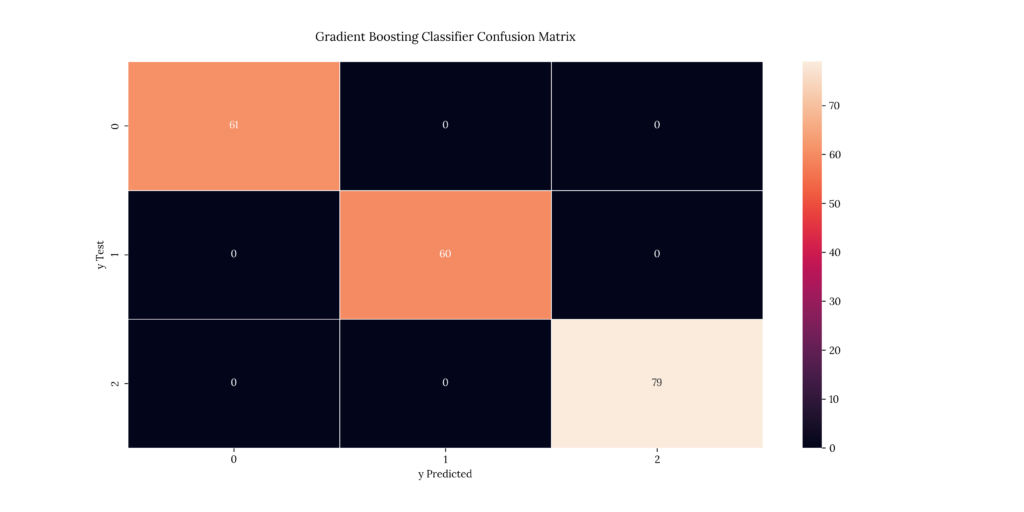
cm_plot('Gradient Boosting Classifier',
model_dictionary['Gradient Boosting Classifier'],
test_Sy,
y_predicted_GBC)
# Define model score
score_GBC = model_score(model_dictionary['Gradient Boosting Classifier'],
test_Sx,
test_Sy)
# Define Classification Report Function
report_GBC = classification_rep(test_Sy,
y_predicted_GBC)
print(score_GBC)If we take a look at our results, we can see that it predicted with a 100% accuracy:
Output
Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 61 |
| 2 | 1 | 1 | 1 | 60 |
| 3 | 1 | 1 | 1 | 79 |
| accuracy | 1 | 1 | 1 | 1 |
| macro avg | 1 | 1 | 1 | 200 |
| weighted avg | 1 | 1 | 1 | 200 |
Output
1.015. Extreme Gradient Boosting
Extreme Gradient Boosting (XGBoost) is a more regularized form of the previous Gradient Boosting technique. This means that it controls overfitting better, resulting in better performance; as opposed to GBM, XGBoost uses advanced regularization (L1 & L2), which improves model generalization capabilities. It also has faster training capabilities and can be parallelized across clusters, reducing training times.
Some other differences between XGBoost over GBM are:
- The use of sparse matrices with sparsity-aware algorithms.
- Improved data structures for better processor cache utilization which makes it faster.
We will skip the mathematical intuition for XGBoost since it’s extensive and similar to its GBM cousin.
15.1 Assumptions
- Encoded integer values for each input variable have an ordinal relationship.
- The data may not be complete (can handle sparsity)
15.2 Implementation
We’ll use a different library called XGBoost for this implementation. Apart from the advantages of the mathematical treatment, XGBoost is written in C++, making it comparatively faster than other Gradient Boosting libraries. Also, XGBoost was specifically designed to support parallelization onto GPUs and computer networks. These make this library extremely powerful when handling extensive data sets.
Before we can start, we will need to re-encode our labels since XGBoost requires our values to start from 0 and not 1:
Code
# Re-encode labels
train_Sy_XGBC = LabelEncoder().fit_transform(train_Sy)
test_Sy_XGBC = LabelEncoder().fit_transform(test_Sy)We will then fit our model to our data:
Code
# Train model
model_dictionary['Extreme Gradient Boosting Classifier'].fit(train_Sx, train_Sy_XGBC)We can then predict some values using our trained model:
Code
# Predict
y_predicted_XGBC = model_dictionary['Extreme Gradient Boosting Classifier'].predict(test_Sx)We can finally evaluate our model using the metrics we defined earlier:
Code
# Evaluate the model and collect the scores
cm_plot('Extreme Gradient Boosting Classifier',
model_dictionary['Extreme Gradient Boosting Classifier'],
test_Sy_XGBC,
y_predicted_XGBC)
# Define model score
score_XGBC = model_score(model_dictionary['Extreme Gradient Boosting Classifier'],
test_Sx,
test_Sy_XGBC)
# Define Classification Report Function
report_XGBC = classification_rep(test_Sy_XGBC,
y_predicted_XGBC)
print(score_XGBC)If we take a look at our results, we can see that it predicted with a 100% accuracy:
Output

Output
| X | precision | recall | f1-score | support |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 61 |
| 1 | 1 | 1 | 1 | 60 |
| 2 | 1 | 1 | 1 | 79 |
| accuracy | 1 | 1 | 1 | 1 |
| macro avg | 1 | 1 | 1 | 200 |
| weighted avg | 1 | 1 | 1 | 200 |
Output
Output
1.016. Deep Neural Networks
Deep Neural Networks are simply Neural Networks containing at least two interconnected layers of neurons. Its functioning and the theory behind them are somewhat different from what we’ve seen so far. Also, they belong to another branch of Artificial Intelligence called Deep Learning, which is itself a subgroup of Neural Networks. The model that would assimilate more (in a sense ) is Decision Trees, although even they process data differently.
Neural Networks were created based on how actual neurons work (in a very general way); they are comprised of node layers containing an input layer, one or more hidden layers, and an output layer. Each node connects to another and has an associated weight and threshold. These parameters define the signal intensity from one neuron to another; if the output of a given individual node is above the specified threshold value, that node is activated, sending a signal to the next layer of the network; else, the signal doesn’t pass through.
Although Deep Neural Networks can achieve complex classification tasks, there are some significant disadvantages:
- It takes time and domain knowledge to fine-tune a Neural Network.
- They’re sensitive to data inputs.
- They are computationally expensive, making them challenging to deploy in a production environment.
- Their hidden layers work as black boxes, making them hard to understand or debug.
- Most of the time, they require more data to return accurate results.
- They rely more on training data, potentially leading to overfitting.
A simpler alternative, such as the Decision Tree Classifier, often gives better accuracy without all the disadvantages above.
Apart from all the points mentioned, there are also significant advantages:
- They can perform unsupervised learning.
- They have good fault tolerance, meaning the output is not affected by the corruption of one or more than one cell.
- They have distributed memory capabilities.
16.1 Mathematical intuition overview
As we have mentioned, a Neural Network works by propagating signals depending on the weight and threshold of each neuron.
The most basic Neural Network is called perceptron and consists of ![]() number of inputs, one neuron, and one output.
number of inputs, one neuron, and one output.
A perceptron’s forward propagation starts by weighting each input and adding all the multiplied values. Weights decide how much influence the given input will have on the neuron’s output:
![]()
Where:
 is a vector of inputs.
is a vector of inputs.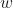 is a vector of weights.
is a vector of weights. is the dot product between
is the dot product between  and
and 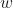 .
.
Then, a bias is added to the summation calculated before:
![]()
Where:
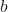 is the bias
is the bias
Finally, we pass ![]() to a non-linear activation function. Perceptrons have binary step functions as their activation functions. This is the most simple type of function; it produces a binary output:
to a non-linear activation function. Perceptrons have binary step functions as their activation functions. This is the most simple type of function; it produces a binary output:
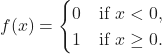
A perceptron is the simplest case, and of course, the more layers we have, the more complex the mathematical derivation gets. Also, more complex and appropriate activation functions are available since the binary activation functions present important disadvantages.
The theory behind Deep Neural Networks is extensive and complex, so we will not explain each step in detail; instead, we will stick with a general description of what is being done. A rigorous & exhaustive explanation of these models can be found in Philipp Christian Petersen’s Neural Network Theory.
16.2 Assumptions
- Artificial Neurons are arranged in layers, which are sequentially arranged.
- Neurons within the same layer do not interact or communicate with each other.
- All inputs enter the network through the input layer and pass through the output layer.
- All hidden layers at the same level should have the same activation function.
- Artificial neurons at consecutive layers are densely connected.
- Every inter-connected neural network has its weight and bias associated with it.
16.3 Implementation
Deep Neural Networks require a different treatment than we’ve already seen. For this case, a simpler 5-layer Sequential model will suffice. The first thing we’ll need to do is define which model we will use.
A Sequential Neural Network passes on the data and flows in sequential order from top to bottom until the data reaches the end of the model.
We can start by making defining our model:
Code
# Define model
DNN = model_dictionary['Sequential Deep Neural Network']Then, we can add the first two dense layers, both using ![]() (Rectified Linear Unit) activation functions:
(Rectified Linear Unit) activation functions:
Code
# Add first two layers using ReLU activation function
DNN.add(Dense(8, activation = "relu", input_dim = train_Sx.shape[1]))
DNN.add(Dense(16, activation = "relu"))Next, we will add a ![]() regularization layer. A dropout layer randomly sets input units to 0 with a frequency rate between 0 and 1 at each step during training time. This helps prevent overfitting:
regularization layer. A dropout layer randomly sets input units to 0 with a frequency rate between 0 and 1 at each step during training time. This helps prevent overfitting:
Code
# Add Dropout regularization layer
DNN.add(Dropout(0.1))We will conclude with our model by adding one last dense ![]() activation layer and one dense
activation layer and one dense ![]() (normalized exponential function) activation layer, which will serve as the activation function for our output layer. The
(normalized exponential function) activation layer, which will serve as the activation function for our output layer. The ![]() activation function converts an input vector of real values to an output vector that can be interpreted as categorical probabilities. It is specially used for categorical variables:
activation function converts an input vector of real values to an output vector that can be interpreted as categorical probabilities. It is specially used for categorical variables:
Code
# Add third layer using ReLU, and output layer using softmax
DNN.add(Dense(8, activation = "relu"))
DNN.add(Dense(3, activation = "softmax"))We will finally compile our model using ![]() as our loss function and
as our loss function and ![]() (adaptive moment estimation) as our optimization function. The
(adaptive moment estimation) as our optimization function. The ![]() loss, also called
loss, also called ![]() , is a
, is a ![]() activation plus a
activation plus a ![]() . It is used for categorical multi-class classification and accepts labels as one-hot encoded. The
. It is used for categorical multi-class classification and accepts labels as one-hot encoded. The ![]() optimizer is an extension to stochastic gradient descent:
optimizer is an extension to stochastic gradient descent:
Code
# Compile our model
DNN.compile(optimizer = "adam", loss = "categorical_crossentropy", metrics = ["accuracy"])Below is a summary of our Deep Neural Network architecture:
- Layer 1:
- Dense with 8 nodes.
- Serves as our input layer as well as our first hidden layer.
- Its shape is given by the feature DataFrame dimensions.
- Uses
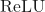 activation function.
activation function.
- Layer 2:
- Dense with 16 nodes.
- Serves as our second hidden layer.
- Uses
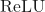 activation function.
activation function.
- Layer 3:
- Dropout with
 , meaning 1 in 10 inputs will be randomly excluded from each update cycle.
, meaning 1 in 10 inputs will be randomly excluded from each update cycle. - Serves as our third hidden layer.
- Dropout with
- Layer 4:
- Dense with 8 nodes.
- Serves as our fourth hidden layer.
- Uses
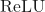 activation function.
activation function.
- Layer 5:
- Dense with 3 nodes, meaning 3 categorical outputs to be predicted.
- Uses
 activation function
activation function
- Compiled model:
- Is Sequential.
- Uses the
 optimizer.
optimizer. - Uses a
 loss function.
loss function.
Before training our model, we will need to re-encode & dummify our labels:
Code
# Re-encode & dummify labels
df_y_D = LabelEncoder().fit_transform(df_y)
df_y_D = pd.get_dummies(df_y_D)We will then fit our model:
Code
# Fit our compiled model
DNN_Fit = DNN.fit(df_x, df_y_D, epochs = 150, validation_split = 0.3)Output
Epoch 1/150
22/22 [==============================] - 0s 6ms/step - loss: 1.1964 - accuracy: 0.3643 - val_loss: 0.9955 - val_accuracy: 0.3967
Epoch 2/150
22/22 [==============================] - 0s 2ms/step - loss: 1.0430 - accuracy: 0.3871 - val_loss: 0.9412 - val_accuracy: 0.4600
Epoch 3/150
22/22 [==============================] - 0s 2ms/step - loss: 0.9726 - accuracy: 0.4986 - val_loss: 0.9127 - val_accuracy: 0.5367
Epoch 4/150
22/22 [==============================] - 0s 2ms/step - loss: 0.9428 - accuracy: 0.5214 - val_loss: 0.8785 - val_accuracy: 0.5733
Epoch 5/150
22/22 [==============================] - 0s 2ms/step - loss: 0.8994 - accuracy: 0.5729 - val_loss: 0.8400 - val_accuracy: 0.5833
Epoch 6/150
22/22 [==============================] - 0s 2ms/step - loss: 0.8901 - accuracy: 0.5843 - val_loss: 0.8042 - val_accuracy: 0.6400
Epoch 7/150
22/22 [==============================] - 0s 2ms/step - loss: 0.8438 - accuracy: 0.6057 - val_loss: 0.7630 - val_accuracy: 0.6500
Epoch 8/150
22/22 [==============================] - 0s 2ms/step - loss: 0.8136 - accuracy: 0.6471 - val_loss: 0.7340 - val_accuracy: 0.6800
Epoch 9/150
22/22 [==============================] - 0s 2ms/step - loss: 0.7942 - accuracy: 0.6271 - val_loss: 0.7032 - val_accuracy: 0.7200
Epoch 10/150
22/22 [==============================] - 0s 2ms/step - loss: 0.7768 - accuracy: 0.6457 - val_loss: 0.6817 - val_accuracy: 0.7067
Epoch 11/150
22/22 [==============================] - 0s 2ms/step - loss: 0.7246 - accuracy: 0.6871 - val_loss: 0.6524 - val_accuracy: 0.7600
Epoch 12/150
22/22 [==============================] - 0s 2ms/step - loss: 0.7206 - accuracy: 0.7086 - val_loss: 0.6272 - val_accuracy: 0.7367
Epoch 13/150
22/22 [==============================] - 0s 2ms/step - loss: 0.6841 - accuracy: 0.7086 - val_loss: 0.6084 - val_accuracy: 0.7700
Epoch 14/150
22/22 [==============================] - 0s 2ms/step - loss: 0.6706 - accuracy: 0.7171 - val_loss: 0.5760 - val_accuracy: 0.7967
Epoch 15/150
22/22 [==============================] - 0s 2ms/step - loss: 0.6454 - accuracy: 0.7371 - val_loss: 0.5556 - val_accuracy: 0.8200
Epoch 16/150
22/22 [==============================] - 0s 2ms/step - loss: 0.6189 - accuracy: 0.7371 - val_loss: 0.5415 - val_accuracy: 0.7967
Epoch 17/150
22/22 [==============================] - 0s 2ms/step - loss: 0.6040 - accuracy: 0.7500 - val_loss: 0.5121 - val_accuracy: 0.7567
Epoch 18/150
22/22 [==============================] - 0s 2ms/step - loss: 0.5769 - accuracy: 0.7586 - val_loss: 0.4923 - val_accuracy: 0.8133
Epoch 19/150
22/22 [==============================] - 0s 2ms/step - loss: 0.5599 - accuracy: 0.7643 - val_loss: 0.4731 - val_accuracy: 0.7833
Epoch 20/150
22/22 [==============================] - 0s 2ms/step - loss: 0.5339 - accuracy: 0.7757 - val_loss: 0.4536 - val_accuracy: 0.8133
Epoch 21/150
22/22 [==============================] - 0s 2ms/step - loss: 0.5142 - accuracy: 0.7814 - val_loss: 0.4372 - val_accuracy: 0.8300
Epoch 22/150
22/22 [==============================] - 0s 2ms/step - loss: 0.5214 - accuracy: 0.7929 - val_loss: 0.4202 - val_accuracy: 0.8767
Epoch 23/150
22/22 [==============================] - 0s 2ms/step - loss: 0.4892 - accuracy: 0.7957 - val_loss: 0.4068 - val_accuracy: 0.7800
Epoch 24/150
22/22 [==============================] - 0s 2ms/step - loss: 0.4669 - accuracy: 0.8071 - val_loss: 0.3943 - val_accuracy: 0.8533
Epoch 25/150
22/22 [==============================] - 0s 2ms/step - loss: 0.4572 - accuracy: 0.8243 - val_loss: 0.3826 - val_accuracy: 0.8400
Epoch 26/150
22/22 [==============================] - 0s 2ms/step - loss: 0.4411 - accuracy: 0.8171 - val_loss: 0.3701 - val_accuracy: 0.7900
Epoch 27/150
22/22 [==============================] - 0s 2ms/step - loss: 0.4304 - accuracy: 0.8314 - val_loss: 0.3587 - val_accuracy: 0.8400
Epoch 28/150
22/22 [==============================] - 0s 2ms/step - loss: 0.4302 - accuracy: 0.8343 - val_loss: 0.3470 - val_accuracy: 0.9033
Epoch 29/150
22/22 [==============================] - 0s 2ms/step - loss: 0.4032 - accuracy: 0.8643 - val_loss: 0.3367 - val_accuracy: 0.9033
Epoch 30/150
22/22 [==============================] - 0s 2ms/step - loss: 0.4106 - accuracy: 0.8471 - val_loss: 0.3283 - val_accuracy: 0.8533
Epoch 31/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3970 - accuracy: 0.8543 - val_loss: 0.3197 - val_accuracy: 0.8933
Epoch 32/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3964 - accuracy: 0.8414 - val_loss: 0.3114 - val_accuracy: 0.8933
Epoch 33/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3795 - accuracy: 0.8614 - val_loss: 0.2986 - val_accuracy: 0.9300
Epoch 34/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3663 - accuracy: 0.8800 - val_loss: 0.2885 - val_accuracy: 0.9300
Epoch 35/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3590 - accuracy: 0.8786 - val_loss: 0.2829 - val_accuracy: 0.8933
Epoch 36/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3729 - accuracy: 0.8671 - val_loss: 0.2737 - val_accuracy: 0.9300
Epoch 37/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3536 - accuracy: 0.8614 - val_loss: 0.2659 - val_accuracy: 0.9300
Epoch 38/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3436 - accuracy: 0.8700 - val_loss: 0.2655 - val_accuracy: 0.9033
Epoch 39/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3260 - accuracy: 0.8829 - val_loss: 0.2550 - val_accuracy: 0.9300
Epoch 40/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3210 - accuracy: 0.9000 - val_loss: 0.2519 - val_accuracy: 0.9300
Epoch 41/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3401 - accuracy: 0.8714 - val_loss: 0.2525 - val_accuracy: 0.8633
Epoch 42/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2945 - accuracy: 0.8957 - val_loss: 0.2467 - val_accuracy: 0.8633
Epoch 43/150
22/22 [==============================] - 0s 2ms/step - loss: 0.3014 - accuracy: 0.8900 - val_loss: 0.2291 - val_accuracy: 0.9400
Epoch 44/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2970 - accuracy: 0.8914 - val_loss: 0.2270 - val_accuracy: 0.9600
Epoch 45/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2764 - accuracy: 0.9029 - val_loss: 0.2181 - val_accuracy: 0.9600
Epoch 46/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2774 - accuracy: 0.9171 - val_loss: 0.2132 - val_accuracy: 0.9600
Epoch 47/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2787 - accuracy: 0.9071 - val_loss: 0.2091 - val_accuracy: 0.9600
Epoch 48/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2893 - accuracy: 0.8971 - val_loss: 0.2058 - val_accuracy: 0.9600
Epoch 49/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2826 - accuracy: 0.8986 - val_loss: 0.2049 - val_accuracy: 0.9600
Epoch 50/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2684 - accuracy: 0.9043 - val_loss: 0.1988 - val_accuracy: 0.9600
Epoch 51/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2594 - accuracy: 0.9186 - val_loss: 0.1996 - val_accuracy: 0.9600
Epoch 52/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2597 - accuracy: 0.9157 - val_loss: 0.1939 - val_accuracy: 0.9600
Epoch 53/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2674 - accuracy: 0.9086 - val_loss: 0.1891 - val_accuracy: 0.9600
Epoch 54/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2608 - accuracy: 0.9129 - val_loss: 0.1852 - val_accuracy: 0.9600
Epoch 55/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2460 - accuracy: 0.9143 - val_loss: 0.1840 - val_accuracy: 0.9600
Epoch 56/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2544 - accuracy: 0.9186 - val_loss: 0.1809 - val_accuracy: 0.9600
Epoch 57/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2419 - accuracy: 0.9200 - val_loss: 0.1799 - val_accuracy: 0.9600
Epoch 58/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2395 - accuracy: 0.9086 - val_loss: 0.1761 - val_accuracy: 0.9600
Epoch 59/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2383 - accuracy: 0.9114 - val_loss: 0.1728 - val_accuracy: 0.9600
Epoch 60/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2389 - accuracy: 0.9114 - val_loss: 0.1691 - val_accuracy: 0.9600
Epoch 61/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2411 - accuracy: 0.9171 - val_loss: 0.1680 - val_accuracy: 0.9600
Epoch 62/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2472 - accuracy: 0.9071 - val_loss: 0.1678 - val_accuracy: 0.9600
Epoch 63/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2140 - accuracy: 0.9229 - val_loss: 0.1699 - val_accuracy: 0.9600
Epoch 64/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2362 - accuracy: 0.9129 - val_loss: 0.1635 - val_accuracy: 0.9600
Epoch 65/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2199 - accuracy: 0.9314 - val_loss: 0.1638 - val_accuracy: 0.9700
Epoch 66/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2270 - accuracy: 0.9200 - val_loss: 0.1539 - val_accuracy: 0.9700
Epoch 67/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2263 - accuracy: 0.9243 - val_loss: 0.1531 - val_accuracy: 0.9600
Epoch 68/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2363 - accuracy: 0.9071 - val_loss: 0.1525 - val_accuracy: 0.9600
Epoch 69/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2056 - accuracy: 0.9329 - val_loss: 0.1476 - val_accuracy: 0.9700
Epoch 70/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2016 - accuracy: 0.9343 - val_loss: 0.1443 - val_accuracy: 0.9700
Epoch 71/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2262 - accuracy: 0.9243 - val_loss: 0.1434 - val_accuracy: 0.9600
Epoch 72/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2043 - accuracy: 0.9371 - val_loss: 0.1485 - val_accuracy: 0.9600
Epoch 73/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2023 - accuracy: 0.9329 - val_loss: 0.1361 - val_accuracy: 0.9600
Epoch 74/150
22/22 [==============================] - 0s 2ms/step - loss: 0.2071 - accuracy: 0.9171 - val_loss: 0.1358 - val_accuracy: 0.9600
Epoch 75/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1905 - accuracy: 0.9286 - val_loss: 0.1285 - val_accuracy: 0.9700
Epoch 76/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1780 - accuracy: 0.9286 - val_loss: 0.1301 - val_accuracy: 0.9867
Epoch 77/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1859 - accuracy: 0.9443 - val_loss: 0.1224 - val_accuracy: 0.9867
Epoch 78/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1764 - accuracy: 0.9371 - val_loss: 0.1251 - val_accuracy: 0.9867
Epoch 79/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1901 - accuracy: 0.9357 - val_loss: 0.1146 - val_accuracy: 0.9867
Epoch 80/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1672 - accuracy: 0.9500 - val_loss: 0.1103 - val_accuracy: 0.9867
Epoch 81/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1693 - accuracy: 0.9414 - val_loss: 0.1093 - val_accuracy: 0.9867
Epoch 82/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1764 - accuracy: 0.9429 - val_loss: 0.1065 - val_accuracy: 0.9867
Epoch 83/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1694 - accuracy: 0.9486 - val_loss: 0.1038 - val_accuracy: 0.9867
Epoch 84/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1666 - accuracy: 0.9529 - val_loss: 0.1140 - val_accuracy: 0.9467
Epoch 85/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1829 - accuracy: 0.9400 - val_loss: 0.0973 - val_accuracy: 0.9867
Epoch 86/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1432 - accuracy: 0.9614 - val_loss: 0.0950 - val_accuracy: 0.9867
Epoch 87/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1502 - accuracy: 0.9614 - val_loss: 0.0924 - val_accuracy: 0.9867
Epoch 88/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1630 - accuracy: 0.9386 - val_loss: 0.0934 - val_accuracy: 0.9867
Epoch 89/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1558 - accuracy: 0.9471 - val_loss: 0.0943 - val_accuracy: 0.9633
Epoch 90/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1529 - accuracy: 0.9543 - val_loss: 0.0856 - val_accuracy: 0.9867
Epoch 91/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1563 - accuracy: 0.9514 - val_loss: 0.0852 - val_accuracy: 0.9867
Epoch 92/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1481 - accuracy: 0.9600 - val_loss: 0.0828 - val_accuracy: 0.9933
Epoch 93/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1333 - accuracy: 0.9643 - val_loss: 0.0829 - val_accuracy: 0.9867
Epoch 94/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1366 - accuracy: 0.9643 - val_loss: 0.0793 - val_accuracy: 0.9933
Epoch 95/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1353 - accuracy: 0.9629 - val_loss: 0.0823 - val_accuracy: 0.9767
Epoch 96/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1273 - accuracy: 0.9671 - val_loss: 0.0776 - val_accuracy: 0.9867
Epoch 97/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1388 - accuracy: 0.9500 - val_loss: 0.0755 - val_accuracy: 0.9933
Epoch 98/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1349 - accuracy: 0.9657 - val_loss: 0.0733 - val_accuracy: 0.9867
Epoch 99/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1198 - accuracy: 0.9600 - val_loss: 0.0702 - val_accuracy: 0.9933
Epoch 100/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1276 - accuracy: 0.9657 - val_loss: 0.0687 - val_accuracy: 0.9867
Epoch 101/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1298 - accuracy: 0.9629 - val_loss: 0.0701 - val_accuracy: 0.9867
Epoch 102/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1092 - accuracy: 0.9686 - val_loss: 0.0734 - val_accuracy: 0.9933
Epoch 103/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1232 - accuracy: 0.9614 - val_loss: 0.0729 - val_accuracy: 0.9867
Epoch 104/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1154 - accuracy: 0.9714 - val_loss: 0.0661 - val_accuracy: 0.9933
Epoch 105/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1138 - accuracy: 0.9700 - val_loss: 0.0609 - val_accuracy: 0.9933
Epoch 106/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1202 - accuracy: 0.9643 - val_loss: 0.0633 - val_accuracy: 0.9867
Epoch 107/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1128 - accuracy: 0.9657 - val_loss: 0.0599 - val_accuracy: 0.9933
Epoch 108/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1131 - accuracy: 0.9743 - val_loss: 0.0583 - val_accuracy: 0.9867
Epoch 109/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1015 - accuracy: 0.9686 - val_loss: 0.0574 - val_accuracy: 0.9933
Epoch 110/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1164 - accuracy: 0.9671 - val_loss: 0.0597 - val_accuracy: 0.9867
Epoch 111/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1072 - accuracy: 0.9671 - val_loss: 0.0575 - val_accuracy: 0.9933
Epoch 112/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1007 - accuracy: 0.9729 - val_loss: 0.0568 - val_accuracy: 0.9933
Epoch 113/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1103 - accuracy: 0.9729 - val_loss: 0.0520 - val_accuracy: 0.9933
Epoch 114/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1025 - accuracy: 0.9729 - val_loss: 0.0529 - val_accuracy: 0.9933
Epoch 115/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0866 - accuracy: 0.9729 - val_loss: 0.0530 - val_accuracy: 0.9933
Epoch 116/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0949 - accuracy: 0.9714 - val_loss: 0.0555 - val_accuracy: 0.9933
Epoch 117/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0967 - accuracy: 0.9686 - val_loss: 0.0474 - val_accuracy: 0.9933
Epoch 118/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1023 - accuracy: 0.9714 - val_loss: 0.0479 - val_accuracy: 0.9933
Epoch 119/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1047 - accuracy: 0.9729 - val_loss: 0.0473 - val_accuracy: 0.9933
Epoch 120/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1154 - accuracy: 0.9643 - val_loss: 0.0603 - val_accuracy: 0.9933
Epoch 121/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1046 - accuracy: 0.9657 - val_loss: 0.0505 - val_accuracy: 0.9867
Epoch 122/150
22/22 [==============================] - 0s 2ms/step - loss: 0.1065 - accuracy: 0.9643 - val_loss: 0.0467 - val_accuracy: 0.9933
Epoch 123/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0988 - accuracy: 0.9700 - val_loss: 0.0442 - val_accuracy: 0.9933
Epoch 124/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0812 - accuracy: 0.9757 - val_loss: 0.0436 - val_accuracy: 0.9933
Epoch 125/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0962 - accuracy: 0.9743 - val_loss: 0.0469 - val_accuracy: 0.9933
Epoch 126/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0841 - accuracy: 0.9786 - val_loss: 0.0421 - val_accuracy: 0.9933
Epoch 127/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0951 - accuracy: 0.9757 - val_loss: 0.0420 - val_accuracy: 0.9933
Epoch 128/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0892 - accuracy: 0.9743 - val_loss: 0.0397 - val_accuracy: 0.9933
Epoch 129/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0760 - accuracy: 0.9771 - val_loss: 0.0381 - val_accuracy: 0.9933
Epoch 130/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0781 - accuracy: 0.9771 - val_loss: 0.0368 - val_accuracy: 0.9933
Epoch 131/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0854 - accuracy: 0.9714 - val_loss: 0.0428 - val_accuracy: 0.9933
Epoch 132/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0747 - accuracy: 0.9729 - val_loss: 0.0336 - val_accuracy: 0.9933
Epoch 133/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0740 - accuracy: 0.9771 - val_loss: 0.0336 - val_accuracy: 0.9933
Epoch 134/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0872 - accuracy: 0.9771 - val_loss: 0.0348 - val_accuracy: 0.9933
Epoch 135/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0750 - accuracy: 0.9814 - val_loss: 0.0321 - val_accuracy: 0.9933
Epoch 136/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0722 - accuracy: 0.9771 - val_loss: 0.0327 - val_accuracy: 0.9933
Epoch 137/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0807 - accuracy: 0.9757 - val_loss: 0.0353 - val_accuracy: 0.9933
Epoch 138/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0762 - accuracy: 0.9786 - val_loss: 0.0322 - val_accuracy: 0.9933
Epoch 139/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0699 - accuracy: 0.9771 - val_loss: 0.0303 - val_accuracy: 0.9933
Epoch 140/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0627 - accuracy: 0.9829 - val_loss: 0.0282 - val_accuracy: 0.9933
Epoch 141/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0784 - accuracy: 0.9757 - val_loss: 0.0272 - val_accuracy: 0.9933
Epoch 142/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0748 - accuracy: 0.9800 - val_loss: 0.0289 - val_accuracy: 0.9933
Epoch 143/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0770 - accuracy: 0.9757 - val_loss: 0.0271 - val_accuracy: 0.9933
Epoch 144/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0629 - accuracy: 0.9800 - val_loss: 0.0276 - val_accuracy: 0.9933
Epoch 145/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0634 - accuracy: 0.9800 - val_loss: 0.0260 - val_accuracy: 0.9933
Epoch 146/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0799 - accuracy: 0.9743 - val_loss: 0.0279 - val_accuracy: 0.9933
Epoch 147/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0723 - accuracy: 0.9771 - val_loss: 0.0252 - val_accuracy: 0.9933
Epoch 148/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0556 - accuracy: 0.9800 - val_loss: 0.0235 - val_accuracy: 0.9933
Epoch 149/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0525 - accuracy: 0.9857 - val_loss: 0.0235 - val_accuracy: 0.9933
Epoch 150/150
22/22 [==============================] - 0s 2ms/step - loss: 0.0597 - accuracy: 0.9800 - val_loss: 0.0225 - val_accuracy: 0.9933This output displays each epoch, the training accuracy achieved, the validation accuracy achieved, and the loss for each step. Here we can see that 150 epochs were barely enough for our model to achieve a training accuracy of 100%. We can also see that in the beginning, our accuracy increases at a higher rate; this makes sense since the gradient for the first epochs is bigger, as we’ll confirm shortly using visualization methods.
We can get a model summary:
Code
# Get model summary
DNN.summary()Output
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 8) 88
dense_1 (Dense) (None, 16) 144
dropout (Dropout) (None, 16) 0
dense_2 (Dense) (None, 8) 136
dense_3 (Dense) (None, 3) 27
=================================================================
Total params: 395
Trainable params: 395
Non-trainable params: 0
_________________________________________________________________We can visualize the 5 layers previously specified, their shape, the number of parameters (inputs) for each layer and the total number of trainable parameters.
We will save this summary as a DataFrame object so we can export it later and add it to our client’s report:
Code
# Convert model summary to DataFrame object
stringlist = []
DNN.summary(print_fn=lambda x: stringlist.append(x))
summ_string = "\n".join(stringlist)
print(summ_string)
table = stringlist[1:-4][1::2]
new_table = []
for entry in table:
entry = re.split(r'\s{2,}', entry)[:-1]
new_table.append(entry)
DNN_summary = pd.DataFrame(new_table[1:], columns=new_table[0])We can plot our Deep neural Network architecture using the visualkeras module:
Code
visualkeras.layered_view(DNN,
legend=True,
to_file='plots/' + 'Deep Neural Network_Model.png',
scale_z=5,
spacing=30)Output

We can also create two plots to help us visualize how our model performed. The first one will plot epochs on the ![]() axis and training accuracy & validation accuracy on the
axis and training accuracy & validation accuracy on the ![]() axis. The second one will plot epochs on the
axis. The second one will plot epochs on the ![]() axis and training & validation loss on the
axis and training & validation loss on the ![]() axis:
axis:
Code
# Plot epochs vs training accuracy & validation accuracy
plt.figure('Epochs vs Accuracy')
plt.xlabel("Number of Epochs")
plt.ylabel("Accuracy of Data")
plt.plot(DNN_Fit.history["accuracy"], label = "Training Accuracy", color = 'k', linewidth = 0.7, marker = 'o', markersize=2)
plt.plot(DNN_Fit.history["val_accuracy"],label = "Validation Accuracy", color = '#24c98d', linewidth = 0.7, marker = 'o', markersize=2)
plt.title("Training Vs. Validation Accuracy")
plt.legend()
plt.savefig('plots/' + 'Deep Neural Network_Epochs vs Accuracy_tp.png', format = 'png', dpi = 300, transparent = True)
plt.close()
# Plot training vs validation loss
plt.figure('Training vs Validation Loss')
plt.xlabel("Number of Epochs")
plt.ylabel("Loss in Data")
plt.plot(DNN_Fit.history["loss"], label= "Training Loss", color = 'k', linewidth = 0.7, marker = 'o', markersize=2)
plt.plot(DNN_Fit.history["val_loss"], label= "Validation Loss", color = '#24c98d', linewidth = 0.7, marker = 'o', markersize=2)
plt.title("Training Vs. Validation loss")
plt.legend()
plt.savefig('plots/' + 'Deep Neural Network_Training vs Validation Loss_tp.png', format = 'png', dpi = 300, transparent = True)
plt.close()Output

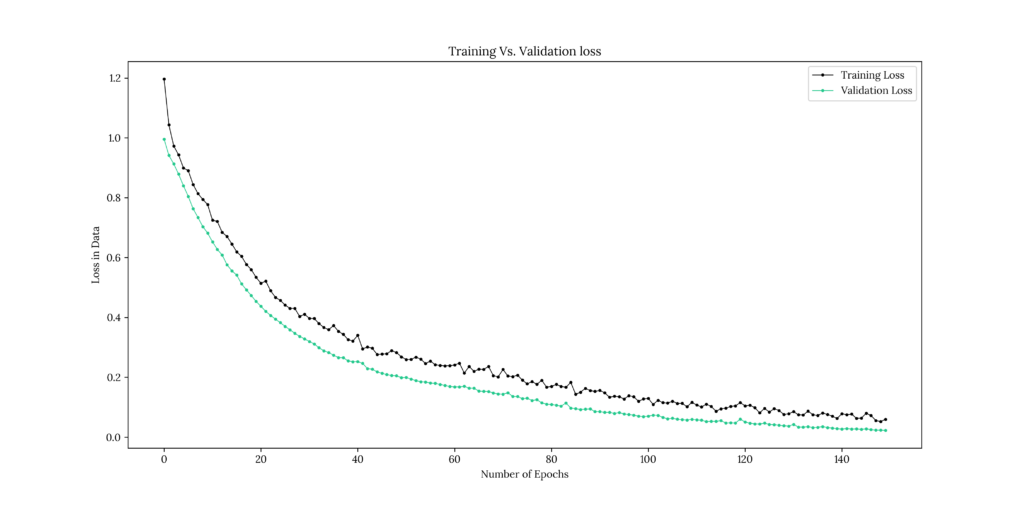
Finally, we will perform a k-fold Cross-validation on our data. This methodology is used to estimate the model accuracy on new data; it splits our data into ![]() groups of samples, also called folds. The model is trained using
groups of samples, also called folds. The model is trained using ![]() of the folds as training data, and the resulting model is validated on the remaining part of the data.
of the folds as training data, and the resulting model is validated on the remaining part of the data.
We can use the KFold method from the sklearn.model_selection library to implement a K-Folds validation. We will start with ![]() folds and our original Deep Neural Network model and see if the accuracy results are satisfactory:
folds and our original Deep Neural Network model and see if the accuracy results are satisfactory:
Code
# Define 10-fold cross validation test harness
kfold = KFold(n_splits=10, shuffle=True)
DNN_accuracy_scores = []
DNN_loss = []
for train, test in kfold.split(df_x, df_y_D):
# Create model
DNN = Sequential()
DNN.add(Dense(8, activation = "relu", input_dim = train_Sx.shape[1]))
DNN.add(Dense(16, activation = "relu"))
DNN.add(Dropout(0.1))
DNN.add(Dense(8, activation = "relu"))
DNN.add(Dense(3, activation = "softmax"))
DNN.compile(optimizer = "adam", loss = "categorical_crossentropy", metrics = ["accuracy"])
# Fit the model
DNN.fit(df_x.iloc[train], df_y_D.iloc[train], epochs=150, verbose=0)
# Evaluate the model
scores = DNN.evaluate(df_x.iloc[test], df_y_D.iloc[test], verbose=0)
print(f'{DNN.metrics_names[0]}: {round(scores[0]*100, 2)}%')
print(f'{DNN.metrics_names[1]}: {round(scores[1]*100, 2)}%')
print('')
DNN_loss.append(scores[0])
DNN_accuracy_scores.append(scores[1])
print(f'{round(np.mean(DNN_accuracy_scores),2)*100}%, +/-{round(np.std(DNN_accuracy_scores),2)*100}%')
DNN_scores_df = pd.DataFrame(columns=['Accuracy', 'Loss'])
DNN_scores_df['Accuracy'] = DNN_accuracy_scores
DNN_scores_df['Loss'] = DNN_lossOutput
loss: 0.71%
accuracy: 100.0%
loss: 1.5%
accuracy: 100.0%
loss: 0.25%
accuracy: 100.0%
loss: 0.28%
accuracy: 100.0%
loss: 3.91%
accuracy: 98.0%
loss: 0.85%
accuracy: 100.0%
loss: 1.32%
accuracy: 100.0%
loss: 0.19%
accuracy: 100.0%
loss: 1.08%
accuracy: 100.0%
loss: 0.15%
accuracy: 100.0%
100.0%, +/-1.0%The Cross-validation analysis gives us two different metrics for ![]() number of folds:
number of folds:
Loss is a value that represents the summation of errors in our model. It measures how well our model is doing. If the errors are high, the loss will be high. In contrast, the lower it is, the better our model works.
Accuracy measures how well our model predicts by comparing the model predictions with the true values in terms of percentage.
17. Results consolidation
Now that we have all the results, we can consolidate them in an Excel sheet using the xlsxwriter engine:
Code
# Create a DataFrame containing accuracy values
acc_list = [score_MLogReg,
score_BLogReg,
score_DecTree,
score_RandomFor,
score_SVM,
score_SVMp,
score_SVMr,
score_KNN,
score_GNB,
score_BNB,
score_SGD,
score_GBC,
score_XGBC,
round(np.mean(DNN_accuracy_scores),2)
]
model_list = list(model_dictionary.keys())
acc_df = pd.DataFrame(columns=['Model', 'Accuracy'])
acc_df['Model'] = model_list
acc_df['Accuracy'] = acc_list
# Write to Excel document
writer = pd.ExcelWriter('outputs/Model_Results.xlsx', engine = 'xlsxwriter')
report_MLogReg.to_excel(writer, sheet_name = 'REP_MLOGREG')
report_BLogReg.to_excel(writer, sheet_name = 'REP_BLOGREG')
report_DecTree.to_excel(writer, sheet_name = 'REP_DECTREE')
report_RandomFor.to_excel(writer, sheet_name = 'REP_RANDOMFOR')
report_SVM.to_excel(writer, sheet_name = 'REP_SVMLIN')
report_SVMp.to_excel(writer, sheet_name = 'REP_SVMPOL')
report_SVMr.to_excel(writer, sheet_name = 'REP_SVMRAD')
report_KNN.to_excel(writer, sheet_name = 'REP_KNN')
report_GNB.to_excel(writer, sheet_name = 'REP_GNB')
report_BNB.to_excel(writer, sheet_name = 'REP_BNB')
report_SGD.to_excel(writer, sheet_name = 'REP_SGD')
report_GBC.to_excel(writer, sheet_name = 'REP_GBC')
report_XGBC.to_excel(writer, sheet_name = 'REP_XGBC')
DNN_summary.to_excel(writer, sheet_name = 'SUM_DNN')
DNN_scores_df.to_excel(writer, sheet_name = 'REP_DNN')
acc_df.to_excel(writer, sheet_name = 'ACC_ALL')
writer.close()18. Method comparison
If we look at our Model_Results.xlsx consolidate, we can see that 8 out of the 14 models we tested predicted the correct Lung Cancer severity level with 100% accuracy. 2 of them presented 91% accuracy, while the other four presented 88%, 85%, 78% and 65% accuracy respectively:
| Model | Accuracy |
|---|---|
| Multinomial Logistic Regressor | 91% |
| Logistic Regressor | 91% |
| Decision Tree Classifier | 100% |
| Random Forest Classifier | 100% |
| Support Vector Classifier | 88% |
| Support Vector Classifier Polynomial Kernel | 100% |
| Support Vector Classifier Radial Kernel | 100% |
| K-Nearest Neighbors Classifier | 100% |
| Gaussian Naïve Bayes Classifier | 65% |
| Bernoulli Naïve Bayes Classifier | 78% |
| Stochastic Gradient Descent | 85% |
| Gradient Boosting Classifier | 100% |
| Extreme Gradient Boosting Classifier | 100% |
| Sequential Deep Neural Network | 100% |
The models who presented the highest accuracy scores were:
- Decision Tree Classifier
- Random Forest Classifier
- Support Vector Classifier Polynomial Kernel
- Support Vector Classifier Radial Kernel
- K-Nearest Neighbors Classifier
- Gradient Boosting Classifier
- Extreme Gradient Boosting Classifier
- Sequential Deep Neural Network
While the models with the lowest prediction accuracy were:
- Stochastic Gradient Descent
- Bernoulli Naïve Bayes Classifier
- Gaussian Naïve Bayes Classifier
In general, the linear models presented lower accuracies, which makes sense since our data has presumably non-linear relationships. In general, most of the non-linear models predicted with 100% accuracy, further sustaining our hypothesis.
Conclusions
In this segment, we reviewed 13 different Machine Learning classification models. First, we performed a general overview of each model and explained the mathematical intuition behind each case. We then tested linear and non-linear implementations.
We also trained and tested a Deep Neural Network model using five layers. We performed a k-folds Cross-validation on it and saw that the accuracies were close to or 100%, meaning our implementation could predict different random subsets of data.
Finally, we compared the prediction accuracies for all of the models and concluded that for our specific data set, there were eight models which scored 100% prediction accuracy.
On the third and final segment of this Guided Project series, we will use everything that we’ve gathered so far to build a technical and business-oriented client deliverable using LaTeX and Texmaker.
References
- IBM, KNN
- OpenGenus, Gaussian Naïve Bayes
- OpenGenus, Bernoulli Naïve Bayes
- Michael Fuchs, Introduction to SGD Classifier
- Jerry Friedman, Greedy Function Approximation: A Gradient Boosting Machine
- Machine Learning Mastery, Multinomial Logistic Regression With Python
- Philipp Christian Petersen, Neural Network Theory
- Machine Learning Mastery, Evaluate the Performance of Deep Learning Models in Keras
- Machine Learning Mastery, Gentle Introduction to the Adam Optimization Algorithm for Deep Learning

