We could spend our entire developer’s life using just the basic concepts of any programming language we choose to learn, and there’s nothing wrong with that; in many cases, very powerful concepts have already been abstracted for us, providing a great out-of-the-box experience, particularly with languages such as Python, R, and JavaScript. However, a programmer’s horizon would be limited if we didn’t have advanced techniques to play with because, in the end, programming is about solving problems, and the more creative, the better. These techniques are not only there to make us more efficient in writing code but also in thinking out of the box by using more sophisticated tools.
In this Blog Article, we’ll discuss ten advanced programming techniques that provide different functionalities to our code; they can make our syntax more elegant, expressive, performant, compact, modular, and a bunch of different attributes that we probably didn’t know could be included in the first place. We’ll focus on Scala since many techniques are closely related to functional programming.
We’ll start by providing historical context on each technique, following a formal definition, main advantages, a set of hands-on examples, recommendations & best practices, and popular real-world use cases.
We’ll be using Scala scripts which can be found in the Blog Article Repo.
What to expect
There are simple techniques such as code refactoring, modularization, and anonymous functions to instantly improve our code. However, this segment will introduce advanced programming concepts. Consequently, it’ll be best to have some previous knowledge of functional programming and, ideally, Scala, Haskell, or a similar language.
We will not include any installation processes since this is out of the scope of this segment (a full Scala 3 installation along with sbt and a preferred IDE is assumed). We will also not discuss basic principles such as syntax and compiling since this is also out of the scope of this segment. Instead, we’ll introduce ten techniques and explain why they’re useful, go over each one in detail, provide a set of examples in Scala, depending on the implementation, and provide some recommendations for using each technique, as well as use cases and best practices.
Preparing our environment
As mentioned, we’ll be using Scala for this segment.
We’ll first head to the directory where we wish our project to be created in:
Code
cd ProjectsWe’ll then create a new Scala project by executing the following command in our terminal:
Code
sbt new sbt/scala-seed.g8We’ll name our project whenever sbt requests the project name.
We’ll then open our preferred IDE, import the newly-generated build, and create a new worksheet inside /projectname/src/main/scala.
Code
cd /projectname/src/main/scalaCode
New-Item -ItemType File -Path ".\Sheet.worksheet.sc"We’ll mainly be working on our worksheet. However, all the implementations discussed in this segment can also be included in a .scala file, given that we include the main Object and function inside a Main.scala file, where Main can be any name.
Now that everything is ready, we’ll move to the first technique: Tail recursion.
1. Tail recursion
The idea of tail recursion has been around for a long time. Still, its specific use in functional programming is often credited to the computer scientist Daniel P. Friedman and his colleagues.
In the late 1970s and early 1980s, Friedman and his colleagues developed a series of programming languages based on Scheme, a dialect of Lisp. These languages included several advanced features for functional programming, including tail recursion optimization.
1.1 Definition
Tail recursion is a type of recursion in which the recursive call is the final operation to be performed within the function. As a result, the function’s stack frame can be reused for the next recursive call instead of creating a new stack frame for each recursive call.
This means the function’s stack size remains constant and does not grow with each recursive call, even if the function recurses deeply. In other words, tail recursion optimizes the memory usage of a function by reusing the same stack frame for multiple recursive calls.
1.2 Advantages
A recursive approach is an elegant and often-used technique to simplify complex problems. It is generally useful for facilitating modular design by breaking a complex problem into smaller sub-problems. It also supports the idea of immutability, which means that variables do not change their value at any time.
Tail recursion is a specific type that provides a safer way to perform recursive calls. By keeping the stack constant and reusing the same stack frame for each recursive call, tail recursion avoids the potential for stack overflow errors that can occur with regular recursion. As a result, it is possible to solve large problems without exceeding maximum recursion depths or encountering memory errors.
1.3 Examples
Let us design four tail-recursive implementations, starting with the simpler ones. In every case, we will include a special annotation, @tailrec. This annotation ensures the compiler optimizes our recursive implementation as a tail recursion problem.
It also explicitly tells the reader that our implementation is a tail-recursive one and should be treated as such (it’s important to note that the Scala compiler will most probably treat our function as tail-recursive even if we omit the annotation. The annotation just makes it explicit and ensures that the function is optimized for this end).
1.3.1 Sum of a list
Let us implement a tail-recursive function that calculates the sum of all elements in a given list of integers. The function should take a list as input and return the total sum of its elements.
What we’ll do here is the following:
- Import the
tailrecannotation. - Define two functions:
- The first outer function will accept a list as its only input.
- The second nested function will accept our list and a counter that we will use to keep track of the summation.
- Call our outer function with a list.
We first import the tailrec annotation and define our outer and nested recursive functions:
Code
import scala.annotation.tailrec
def recursiveSum(list: List[Int]): Int = {
@tailrec
def sumItems(list: List[Int], counter: Int): Int = {
if (list.isEmpty) counter
else sumItems(list.tail, counter + list.head)
}
sumItems(list, 0)
}If we noticed, the @tailrec annotation refers to the nested function. This is because the outer function is not tail-recursive. In fact, it’s not even a recursive function; it simply calls the nested function when called.
We can then call our outer function with a simple list first:
Code
recursiveSum(List(1, 2, 3, 4, 5, 6, 7, 8, 9, 10))Output
// res1: Int = 55We can try our function with a larger number:
Code
recursiveSum(List.range(1, 100000))Output
// res2: Int = 704982704But what if we try it with an even larger number?:
Code
recursiveSum(List.range(1, 1000000000))Output
java.lang.OutOfMemoryError: Java heap space: failed reallocation of scalar replaced objectsIn this case, we get a heap memory error. But didn’t we just say that tail recursion maintained stacks as constant, meaning we should not have recursion depth errors? Yes, that’s right, but the problem here is not a stack overflow error.
When we encounter a large list such as the one we defined in our last example, the compiler may have trouble allocating space for the object. While using tail recursion can help avoid stack overflow errors, it doesn’t necessarily prevent memory heap errors; in some cases, a tail-recursive function may still consume a large amount of memory if it creates many intermediate objects that are not garbage collected.
We can see that although extremely useful, tail recursion has limitations. This can be solved by implementing other techniques:
- Processing the list in smaller chunks.
- Using lazy evaluation.
- Use primitive types.
1.3.2 Factorial calculation
Let us implement a tail-recursive function that calculates the factorial of a given non-negative integer ![]() . The factorial of
. The factorial of ![]() (denoted as
(denoted as ![]() ) is the product of all positive integers less than or equal to
) is the product of all positive integers less than or equal to ![]() . For example,
. For example, ![]() .
.
The main problem with a factorial calculation is that it grows fast. In fact, a factorial will eventually grow faster than ![]() and
and ![]() (but not
(but not ![]() ), so we have to find another numeric type that will allow us to store big integers; if we select the conventional
), so we have to find another numeric type that will allow us to store big integers; if we select the conventional Int type, the type will overflow and result in negative values, or in our case, 0.
As with the previous example, we will import the @tailrec annotation and define two functions:
- Import the
tailrecannotation. - Define two functions:
- The first outer function will accept an
Inttype as its only input. - The second nested function will accept our
Inttype value and a counter withBigInttype that we’ll use to keep track of the factorial operation.
- The first outer function will accept an
- Call our outer function with an integer value.
We first import the tailrec annotation and define our outer and nested recursive functions:
Code
def factorialCalc(n: Int): BigInt = {
@tailrec
def factorialItems(n: Int, counter: BigInt): BigInt = {
if (n == 0) 1
else if (n == 1) counter
else factorialItems(n-1, n * counter)
}
factorialItems(n, 1)
}We can start by calling our function using an edge case, which in our case will be 0:
Code
factorialCalc(0)Output
// res1: BigInt = 1We can then call out outer function with a small integer:
Code
factorialCalc(4)Output
// res2: BigInt = 24We can try our function with a larger number:
Code
factorialCalc(10)Output
// res3: BigInt = 3628800And even with a larger number:
Code
factorialCalc(100)Output
// res4: BigInt = 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000We can see that the last output doesn’t even fit in a single line. We would’ve gotten a type overflow if we had not used BigInt.
1.3.3 Fibonacci sequence
Let us implement a tail-recursive function that returns the ![]() number in the Fibonacci sequence. The Fibonacci sequence is a series of numbers in which each is the sum of the two preceding ones, starting from
number in the Fibonacci sequence. The Fibonacci sequence is a series of numbers in which each is the sum of the two preceding ones, starting from ![]() and
and ![]() . For example, the sequence goes
. For example, the sequence goes ![]() , and so on.
, and so on.
Similar to our previous examples, we will proceed as follows:
- Import the
tailrecannotation. - Define two functions:
- The first outer function will accept an
Inttype as its only input. - The second nested function will accept our
Inttype value, a numbernextwithBigInttype, and a numbercurrentwithBigInttype.
- The first outer function will accept an
- Call our outer function with an integer value.
We define a and b as follows:
next: Will be the previous number in our sequence.curr: Will be the current number in our sequence.
We first import the tailrec annotation and define our outer and nested recursive functions:
Code
def FibCalc(n: Int): BigInt = {
@tailrec
def fibItems(n: Int, next: BigInt, current: BigInt): BigInt = {
if (n == 0) current
else fibItems(n-1, next + current, next)
}
fibItems(n, 1, 0)
}Let us exemplify this calculation using a table:
| Index | Next | Current |
|---|---|---|
| 7 | 1 | 0 |
| 6 | 1 (next + current) | 1 (next) |
| 5 | 2 (next + current) | 1 (next) |
| 4 | 3 (next + current) | 2 (next) |
| 3 | 5 (next + current) | 3 (next) |
| 2 | 8 (next + current) | 5 (next) |
| 1 | 13 (next + current) | 8 (next) |
| 0 | 21 (next + current) | 13 (next) |
A step-by-step explanation:
- Initially, we initialize our index with 7, our
nextvalue with 1, and ourcurrentvalue with 0. - We then subtract one from our index, set our new
nexttonext+current, and set our newcurrenttonext. - We do this until our index is 0.
- We finally return
currentas our final value.
What we’re doing here is keeping track of three sequences at the same time:
- A decreasing sequence (
index). - An increasing sequence (
current). - The calculation (
next).
The key thing here is that we don’t return the next value; instead, we return the current value, which is the next value from the previous step.
We can test our algorithm with some smaller and bigger numbers:
Code
// Edge case call
FibCalc(0)
// Small integer call
FibCalc(5)
// Extense call
FibCalc(10)
// Even bigger call
FibCalc(1000)Output
// res6: BigInt = 0
// res7: BigInt = 5
// res8: BigInt = 55
// res9: BigInt = 434665576869374564356885276750406258025646605173717804024817290895365554179490518904038798400792551692959225930803226347752096896232398733224711616429964409065331879382989696499285160037044761377951668492288751.3.4 Exponentiation
Let us implement a tail-recursive function that calculates the result of a given number (base) raised to the power of another number (exponent). The function should take two integer inputs, base, and exponent, and return the result as a single integer.
We’ll take a similar approach to our previous implementations:
- Import the
tailrecannotation. - Define two functions:
- The first outer function will accept two
Inttype variables,baseandexp. - The second nested function will accept our two
Inttype variables,baseandexp, and a counter withBigInttype.
- The first outer function will accept two
- Call our outer function with two integer values.
We first import the tailrec annotation and define our outer and nested recursive functions:
Code
def ExpCalc(base: Int, exp: Int) : BigInt = {
@tailrec
def ExpItems(base: Int, exp: Int, counter: BigInt): BigInt = {
if (base == 0) 0
else if (exp == 0) 1
else if (exp == 1) counter
else ExpItems(base, exp - 1, base*counter)
}
ExpItems(base, exp, base)
}We will then call our function with smaller and bigger numbers:
Code
// Edge case call
ExpCalc(0, 0)
// Small integer call
ExpCalc(2, 2)
// Extense call
ExpCalc(8, 4)
// Even bigger call
ExpCalc(14328, 5)Output
// res1: BigInt = 0
// res2: BigInt = 4
// res3: BigInt = 4096
// res4: BigInt = 6038483225604899143681.4 Recommendations & best practices
As we have seen from our previous examples, some common patterns emerge when using recursion:
- It is important to properly define the edge or boundary case(s) that act as the stopper for the recursion. These cases must be thought out carefully, as any errors in their definition can result in an infinite loop or memory error.
- The function should be recursively called using some kind of modified parameter, which ensures that the problem size is reduced with each recursive call. We eventually reach the edge or boundary case by reducing the problem size, where recursion terminates.
In the case of tail recursion, it is often necessary to define a helper function that provides a counter or accumulator. This is because, in order to avoid any operations at the end beside the recursive call, we need to recursively call our function with modified arguments using a counter to keep track. Without a counter or accumulator, we would lose important tracking parameters in favor of our accumulator. Using a helper function to accumulate the results, we can maintain the necessary tracking parameters while avoiding additional operations at the end of the recursion.
As we have seen, tail recursion is not infallible, and there are some recommendations to follow to ensure proper execution:
- Ensuring tail-call optimization: For tail recursion to work effectively, we must place the recursive call as the last operation in the function. We must ensure that no further operations depend on the result of the recursive call. This allows the compiler to optimize the recursion into a loop, avoiding stack overflow issues.
- Using accumulator variables: We mentioned using counter or accumulator variables to carry the intermediate results through the recursion, reducing the need for additional computation or memory overhead. We can pass these variables as parameters in our recursive implementation.
- Keeping it simple: Tail-recursive functions should be designed with simplicity in mind. We must avoid complex logic or nested conditional statements that can make the code harder to understand and maintain.
- Using helper functions: Using helper functions to encapsulate the tail-recursive logic can make the code more readable and maintainable. It also makes it possible to implement many tail-recursive functions in the first place.
- Documenting our code: Clearly documenting our tail-recursive functions, including a description of the function, input parameters, return values, and any edge cases, will make it easier for others (and ourselves) to understand and maintain the code.
- Testing edge cases: Thoroughly testing our tail-recursive functions with various input values, including edge cases such as negative numbers, zero, and large numbers, will help ensure the correctness and stability of our implementation.
- Considering alternatives: While tail recursion is an effective technique for certain problems, it may not always be the best approach. We must consider alternative algorithms or data structures that might offer better performance or simplicity in some cases.
- Understanding language/compiler limitations: Some programming languages or compilers may not support tail-call optimization. It’s important to be aware of the language or compiler’s limitations and consider alternative approaches if tail-call optimization is not supported or guaranteed.
1.5 Use cases
Apart from the mathematical applications we already reviewed, this technique can be used in a variety of real-life situations:
- Tree traversal: We can use tail recursion to efficiently traverse data structures like trees or graphs in depth-first or breadth-first order, which can be particularly useful in scenarios like searching, sorting, or parsing XML/JSON files.
- Parsing and tokenization: Tail recursion can optimize memory usage and improve performance in parsing and tokenization processes, essential in compiler design when converting a source code file into tokens or parsing an expression.
- String manipulation: Tail recursion can be used for efficient string manipulation tasks like string reversal, pattern matching, or substring search, which are common in text processing scenarios.
- File and directory operations: Tail recursion can optimize memory consumption and improve performance in file system operations such as directory traversal, file search, or file copying.
- Optimization problems: Tail recursion can be applied in dynamic programming or other optimization problems, where a problem is broken down into smaller subproblems and solved iteratively, leading to efficient solutions that avoid redundant calculations and save memory.
2. Higher-order functions
Higher-order functions are often attributed to the mathematician and computer scientist Alonzo Church, who developed lambda calculus in the 1930s. Lambda calculus established a theoretical foundation for functional programming and introduced the concept of higher-order functions. This concept was later popularized in programming languages such as Lisp, created in the late 1950s, and has since become a crucial element of functional programming.
2.1 Definition
Higher-order functions are one of the pinnacles of functional programming. They are very simple yet extremely elegant and, well, functional. A higher-order function is one that accepts and/or returns a function instead of a value. In other words, a higher-order function operates on functions.
This concept is easy to implement in Scala since all functions are first-class citizens of the value type (first-class values), meaning they can be treated as values and be passed as arguments to other functions, returned as values from functions, and assigned to variables.
The basic syntax of a higher-order function is as follows:
Code
// Higher-order function
def myfun(f: Int => Boolean, n: Int): Boolean = {
f(n)
}
// Parameter function
def f(n: Int): Boolean = {
n >= 1
}
// Higher-order function call
myfun(f, 1)- We first define our higher-order function that will accept a function
f. - We then define a function f that accepts an
Intvalue and returns aBooleanvalue. - Lastly, we call our higher-order function with
fas the argument.
2.2 Advantages
Higher-order functions provide an additional layer of abstraction in functional programming, which can be very useful when working with repetitive tasks. They can be combined with tail-recursive methods to provide an elegant and minimalist way to handle complex operations.
One of the key benefits of higher-order functions is their flexibility and conciseness. By separating the logic of a function from its implementation details, we can achieve greater modularity and reuse of code.
While higher-order functions can be tricky to understand initially, working through some simple examples can help clarify their usage and benefits.
2.3 Examples
We’ll review two examples of higher-order function implementations: The first will be a simple case, while the second will be more elaborate.
2.3.1 Single verification of a list
Let us implement a function that accepts a list of integers and a predicate function (Int => Boolean). The function should return the number of occurrences that satisfy the given predicate. The predicate function evaluates to true if the number is even.
We can follow the steps below:
- Define an outer function that will accept a checker function and our list containing the target numbers.
- Define an inner function that recursively goes over all the numbers in the list and passes them as arguments to our predicate function.
- Define a predicate function to evaluate whether a given number is even.
- Return the total number of occurrences by using a counter.
Code
def checkList(checkerEven: Int => Boolean, list: List[Int]): Int = {
def countElements(checkerEven: Int => Boolean, list: List[Int], counter: Int): Int = {
if (list.isEmpty) counter
else {
if (checkerEven(list.head)) countElements(checkerEven, list.tail, counter + 1)
else countElements(checkerEven, list.tail, counter)
}
}
countElements(checkerEven, list, 0)
}
def checkerEven(target: Int): Boolean = {
target % 2 == 0
}If we call our higher-order function, we should get the following:
Code
checkList(checkerEven, List(1, 2, 3, 4, 5, 6, 7, 8, 9, 10))Output
// : Int = 52.3.2 Variation of a summation
Let us define a function that accepts two integers, ![]() ,
, ![]() , as upper and lower bounds, an integer
, as upper and lower bounds, an integer ![]() for performing addition and product operations, and two functions as arguments. The function calculates a variation of the summation operation, where the first argument function will perform the addition operation for each term of the summation between
for performing addition and product operations, and two functions as arguments. The function calculates a variation of the summation operation, where the first argument function will perform the addition operation for each term of the summation between ![]() and
and ![]() , while the second one will calculate the product of the result of the previous operation with the parameter
, while the second one will calculate the product of the result of the previous operation with the parameter ![]() .
.
Similar to the previous example, we can follow the steps below:
- Define the higher-order function that will recursively call all the elements of the list.
- Define a second function that will perform the addition operation.
- Define a third function that performs the product operation.
- Return the resulting value.
Code
def sumNumbers(applyProduct: (Int, Int) => Int, applyAddition: (Int, Int) => Int, a: Int, b: Int, x: Int): Int = {
if (a > b) 0
else applyProduct(applyAddition(a, x), x) + sumNumbers(applyProduct, applyAddition, a + 1, b, x)
}
def applyProduct(n: Int, x: Int): Int = {
n * x
}
def applyAddition(n: Int, x: Int): Int = {
n + x
}Let us explain the process step-by-step:
- We define our three functions:
sumNumbers,applyProduct, andapplyAddition. applyProducttakes twoIntarguments,nandx, and returns their product (n * x).applyAdditiontakes twoIntarguments,nandx, and returns their sum (n + x).sumNumberstakes five arguments: two function arguments,applyProductandapplyAddition, which both have the type signature(Int, Int) => Int, and threeIntarguments,a,b, andx.- In
sumNumbers, we define a conditional expression:- If
a > b, the function returns0. - Else, the function calculates
applyProduct(applyAddition(a, x), x)and adds it to a recursive call ofsumNumberswith the same function arguments andaincremented by1.
- If
We can finally call our function:
Code
sumNumbers(applyProduct, applyAddition, 2, 3, 2)Output
// : Int = 182.4 Recommendations & best practices
- Using clear naming: It’s best to use descriptive names for higher-order functions and their arguments to improve code readability and maintainability.
- Using type annotations: We can specify types for function arguments and return values to ensure type safety and make the code more understandable.
- Keeping functions small and focused: Each function should have a single responsibility. This makes it easier to understand, test, and reuse the functions.
- Leveraging immutability: As with functional programming in general, using immutable data structures and avoiding side effects in higher-order functions can reduce the risk of bugs and improve code predictability.
- Using standard library functions: We can use built-in higher-order functions like
map,filter, andreduceinstead of implementing custom iterations. This leads to cleaner, more idiomatic code.
2.5 Use cases
- Data transformation: Higher-order functions like
mapcan transform data in a collection by applying a specific function to each element. - Filtering data: For refining data, we can use higher-order functions like
filterto include or exclude elements based on a given condition. - Data aggregation: Higher-order functions like
reduceorfoldcan be used for custom aggregations, such as summing or multiplying elements in a collection into a single result. - Function composition: Higher-order functions can create new functions by combining or chaining existing ones, improving code reusability and modularity.
- Event handling: In event-driven programming, higher-order functions can simplify attaching or detaching specific behaviors to events by defining and managing event listeners.
3. Currying
Currying is a technique introduced in the 1930s by the mathematician and logician Haskell Brooks Curry as part of his work in combinatory logic. The concept of currying was further developed in the 1950s and 1960s by other mathematicians and computer scientists, such as Alonzo Church and John McCarthy. It was then popularized in functional programming languages such as Lisp and ML.
3.1 Definition
Currying is a technique that builds on higher-order functions. It involves breaking down a function that takes multiple arguments into a series of functions that take one argument each. The resulting functions can be called sequentially using parentheses. Currying allows for more flexibility in function composition, and it can be particularly useful in functional programming paradigms where functions are first-class citizens.
3.2 Advantages
- Modularity: Currying can break down functions into smaller, more manageable parts, making code easier to read, write, and maintain.
- Flexibility: Currying allows for partial application and composition with other functions, creating new functions from existing ones in a modular and flexible way.
- Code reuse: Currying allows generic functions to be parameterized with specific functionality, reducing code duplication and promoting code reuse.
- Type safety: Currying ensures that functions only accept arguments of the correct type, making code more robust and reducing the likelihood of runtime errors.
- Partial evaluation: Partial evaluation is possible with currying by allowing functions to be evaluated with some of their arguments, reducing the need for repeated computations and improving performance.
3.3 Examples
We’ll perform two examples, the first including a curried function and the second one including a curried call to two functions.
3.3.1 A curried addition function
Let us implement a curried function called add that takes two integer arguments, x and y, and returns their sum. The function should be defined using multiple parameter lists, where the first parameter list takes one integer argument x, and the second parameter list takes one integer argument y. The function should be flexible and modular, allowing it to be partially applied or composed with other functions.
The steps to follow are straightforward:
- Implement a curried function.
- Partially call the curried function.
- Complete the curried function call in a new line.
Code
// Define a curried function
def sumNums(x: Int)(y: Int) = {
x + y
}
// Partial call
val first_call = sumNums(7) _
// Complete call
val second_call = first_call(3)Output
// : Int => Int = <function1>
// : Int = 10We use the _ placeholder to indicate that we want to apply a function with one or more arguments partially. The _ placeholder is used in place of the argument that we want to apply partially, indicating that we’re creating a new function that takes the remaining arguments.
The type of first_call is actually a function we can apply to a given value. If we hover over first_call below the Complete call line, it will tell us the following:
Output
def apply(v1: Int): Int
Apply the body of this function to the argument.
**Returns:** the result of function application.This is interesting because we can apply first_call to any other value and even a function.
3.3.2 A curried call using two functions
Let us define a curried function that computes the sum of two values, ![]() and
and ![]() , and then squares this result.
, and then squares this result.
This one is a little bit trickier since we need to first define a function that accepts the following:
- A function that will square the result.
- Two integers,
 and
and 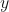 , that will be operated on.
, that will be operated on. - A squaring function that will square the result.
Let us begin with the first one:
Code
def sumInts(squareInt: Int => Int)(x: Int, y: Int): Int = {
squareInt(x + y)
}We can already see that the syntax is slightly different. What we’re doing is:
- Define a curried function
sumIntsthat has two parameter groups.- The first group is actually a function
squareInt, which accepts an integer and returns an integer. - The second group is our
 ,
, 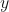 pair.
pair. - The function returns an integer type.
- The first group is actually a function
- Call the
squareIntfunction on the sum of the ,
, 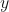 value pair.
value pair.
We then define our squareInt function:
Code
def squareInt(a: Int): Int = {
a*a
}We can finally call our functions:
Code
sumInts(squareInt)(2, 3)This syntax is also slightly unconventional. Let us explain it:
- We first call our
sumIntsfunction with the first group of parameters (i.e., thesquareIntfunction). - We then call our newly composed function with the numbers we wish to operate on.
If we recall anonymous functions, each function inside our call is anonymous, meaning it has no name.
We get the following output in return:
Output
// : Int = 25As with the previous example, we could’ve also performed a partial call, and then use our new function as required:
Code
val applySumSquare = sumInts(squareInt) _Code
applySumSquare(2, 3)Output
// : Int = 25To maximize the benefits of currying in our code, we can consider the following best practices:
- Identifying suitable use cases: Currying can be useful for partial application, function specialization, or enhancing type inference. Identify where these benefits can be applied in our code.
- Thoughtfully ordering parameters: To create partially applied functions more easily, we can arrange parameters in a way that prioritizes those most likely to be reused or pre-filled in the initial groups.
- Avoiding overuse: While currying can be helpful, excessive use can make code harder to read and understand. We must use it thoughtfully and in moderation.
- Combining with other functional techniques: Combining currying with other functional programming techniques, such as function composition and higher-order functions, can further enhance our code’s functionality.
- Keeping function signatures clear: To ensure that function signatures remain clear and understandable, we can provide appropriate type annotations and use descriptive parameter names when utilizing currying.
3.5 Use cases
- Reusable validators: Currying can create reusable validation functions for user inputs in web applications by partially applying common validation rules while leaving the input value to be used later.
- Customized event handlers: In event-driven programming, currying can create customized event handlers with pre-filled arguments, such as the event type or specific settings, allowing flexibility and code reuse.
- Configurable logging: Currying can be leveraged to build configurable logging functions where the log level, message format, or output destination can be partially applied, making it easy to create specialized loggers with minimal code changes.
- Flexible arithmetic operations: In mathematical computations, currying can be utilized to create flexible arithmetic operations, such as specialized adders or multipliers, by partially applying one operand and allowing the other to be applied later.
- Tailored data transformations: In data processing pipelines, currying can be used to generate tailored data transformation functions with specific rules or configurations partially applied, streamlining the process of applying these transformations to various data sets.
4. Monads
Monads are a concept in functional programming originally developed in the 1960s in category theory, a branch of mathematics that studies abstract structures and relationships between them.
The concept in the context of functional programming was rediscovered by the computer scientist Eugenio Moggi, who published a paper in 1989 called “Computational Lambda Calculus and Monads“. Monads were first introduced in Haskell in the early 1990s and still comprise a core part of the language.
4.1 Definition
A monad is an English translation for “monada” in Spanish, which, interestingly enough, means cute little thing (that is, if we eat the accent since my keyboard has US layout and Keychron is to blame) (And no, it’s not a referral link, I genuinely love my keyboard, which I’m sure cannot be said for my family hearing the thick thock at 6 am).
Jokes aside, a monad is a design pattern used to encapsulate and manipulate computations that produce values of a specific type, abstracting away the details of the calculation.
In simpler terms, a monad can be thought of as a “container” or a “wrapper” that holds a value and provides a standardized way to perform operations on that value. Monads are of huge help when chaining computations and handling side effects, making it easier to reason about and structure code.
Monads exist in various languages (mainly in functional ones), such as Haskell, Scala, F#, Swift, JavaScript, Kotlin, Rust, and even Python. While some languages have built-in support for monads, others can utilize monadic concepts through third-party libraries or manually implement monadic patterns.
4.2 Advantages
Monads were introduced to computational theory as a way to handle side effects; if we have a chain of operations represented by functions that will eventually result in a return value, monads make sure that, if a given step produces an unintended value (such as null or nil values), there will be appropriate handling for that, thus avoiding an error return.
More specifically, we usually want to define our chains of operations using functions in functional programming. If we would like to execute a given chain of functions without errors, we could define an intermediate function that handles the types behind the scenes (sort of a checker), so that when we call our chained functions and the first function returns an “unexpected” value, we can handle that within our chain. More importantly, we’re abstracting this concept into a function that can be reused in as many intermediate steps as possible. This could potentially save us a lot of time for exception writing.
Another great example of functional programming is the purity of functions. A function is pure if it returns the same value repeatedly. An impure function might return different values when calling with the same input. We can employ monads to ensure that impure functions return a boxed value (i.e., a value of a primitive type wrapped or “boxed” into an object of a corresponding reference type).
So why go all about this fur when we can simply build an exception handling with conditionals or assertions? Well, there are some advantages to monads that the previous simply cannot offer:
- Explicit error handling: Monads like
Option,Either, andTrymake error handling more explicit by directly encoding the possibility of failure in the type system. - Improved code readability: Monads can make code more readable and maintainable by abstracting away error handling boilerplate. Chaining monadic operations using
flatMap,map, andforcomprehensions can lead to cleaner and more concise code than nested conditionals ortry–catchblocks. - Encapsulation of side effects: Monads can be used to encapsulate side effects, making it easier to reason about the code. This is particularly useful in functional programming, where immutability and the absence of side effects are desired properties. Monads like
IOin Haskell orTaskin Scala help manage side effects in a controlled manner without breaking the functional programming principles. - Composability: Monads are highly composable, allowing us to chain multiple operations together cleanly and concisely. This can lead to more modular and reusable code compared to using conditionals and assertions. Additionally, monads can be used with higher-order functions and other functional programming techniques.
- Avoiding exceptions: Exceptions can be expensive in terms of performance, making it more difficult to reason about the control flow of our program. By using monads, we can return a value representing success or failure and handle errors in a more controlled and predictable manner.
Monads are confusing if explained with simple words. This is why we’ll spend appropriate time exploring one of them with a simple example.
4.3 Examples
Let us explore one case where we have a chain of two functions and would like to ensure proper and smooth execution between them:
4.3.1 An undefined operation
We would like to pack two expressions into two separate functions and perform them consecutively:
- Value A divided y Value B equals Value C.
- Value C divided by Value D equals E.
Code
// Unsafe division one
def unsafeDivOne(UnsafeDivTwo: (Double, Double) => Double, a: Double, b: Double, d: Double): Double = {
UnsafeDivTwo(a, b) / d
}
// Unsafe division two
def UnsafeDivTwo(a: Double, b: Double): Double = {
a / b
}If we call our first function with positive real numbers, we’ll get the expected result:
Code
unsafeDivOne(UnsafeDivTwo, 12, 2, 3)Output
// res1: Double = 2.0However, as simple as this example is, it can easily fail; if we feed 0 to the parameter B, the result of the expression becomes undefined, and the execution returns infinity.
Code
unsafeDivOne(UnsafeDivTwo, 12, 0, 3)Output
// res1: Double = InfinityLet us redefine our unsafe implementations to safe ones:
Code
// Safe division one
def safeDivOne(SafeDivTwo: (Double, Double) => Option[Double], a: Double, b: Double, d: Double): Option[Double] = {
if (b != 0 & d != 0) {
safeDivTwo(a, b).flatMap(result => safeDivTwo(result, d))
}
else None
}
// Safe division two
def safeDivTwo(a: Double, b: Double): Option[Double] = {
if (b != 0) Some(a / b)
else None
}In this solution, we use the Option monad to handle the possibility of a division by zero. Option is a container type representing a value’s presence or absence. It has two subclasses: Some and None.
Some represents a value being present, whereas None represents the absence of a value. Using the Option and the flatMap functions, we can chain operations and handle the absence of a value elegantly and effectively.
This can be a little confusing, so let us explain what we’re doing step-by-step:
- Define the
safeDivOnefunction:- It takes a function
safeDivTwoas a parameter, which has the type(Double, Double) => Option[Double]. - It also takes three
Doubleparameters:a,b, andd.
- It takes a function
- Check if both
banddare non-zero:- If either
bordis zero, the function returnsNoneas a result, indicating that the division cannot be performed. - In this case,
Nonerepresents the absence of a valid division result.
- If either
- If both
banddare non-zero, perform the first division operation:- Call the
safeDivTwofunction withaandbas arguments. - This will return an
Option[Double]representing the result of the first division operation. - If the division is valid, the result is wrapped in a
Some, indicating the presence of a value. Otherwise, it returnsNone.
- Call the
- Chain the second division operation using the
flatMapmethod:- The
flatMapmethod is used on theOption[Double]returned by the first division operation. It helps chain operations when working with monads likeOption. - It takes a function as its argument, which receives the inner value of the
Option[Double](the result of the first division operation) only if it’s aSome. - The function calls
safeDivTwowith the result of the first division anddas arguments. - This will return an
Option[Double]representing the second division operation’s result, wrapping the result in aSomeif the division is valid or returningNoneotherwise.
- The
- Return the final result, which is an
Option[Double]representing the result of both division operations or the absence of a valid result. - Define the
safeDivTwofunction:- It takes two
Doubleparameters:aandb. - It checks if
bis non-zero. - If
bis non-zero, it returnsSome(a / b)as the division result, wrapping the value in aSometo indicate the presence of a valid result. - If
bis zero, it returnsNoneto indicate that the division cannot be performed, representing the absence of a valid result.
- It takes two
- Call the
safeDivOnefunction with thesafeDivTwofunction,12,2, and3as arguments, and store the result in a variable.
We can then call our function with unsafe parameters:
Code
safeDivOne(safeDivTwo, 12, 0, 3)And the output will be what we intended:
Output
// res1: Option[Double] = NoneOf course, there’s no point in making all this effort if the user gets a None value as a result.
This is where our next technique, pattern matching, comes into play.
4.4 Recommendations & best practices
Monads are powerful abstractions that can manage side effects, compose functions, and represent computations, but they enclose an extensive range of topics, such as monoids and functors. It is crucial to have a solid understanding of monads and their functionalities before utilizing them in Scala. Additionally, monadic programming styles rely heavily on this technique.
However, with great power comes great responsibility. To ensure the proper use of monads, here are some best practices and recommendations to follow:
- Choosing the Right Monad: We can select the appropriate monad for the specific use case, such as using Option for handling nullable values, Either for representing computations that can fail, or Future for handling asynchronous operations.
- Chaining Operations: We can use monad’s
flatMap,map, andfiltermethods to chain operations while maintaining the context. This allows for a more concise and readable code, reducing the need for nested pattern matching or manual error handling. - Embracing for-Comprehensions: We can use for-comprehensions to write more readable and concise code when working with multiple monads. It simplifies the chaining of
flatMap,map, andfilteroperations, allowing for a more intuitive expression of the underlying computation. - Error Handling: We can use monads like
Either, pattern match, or fold to properly handle different outcomes. This ensures that errors are dealt with in a type-safe and structured manner, allowing for better overall error handling within the application. - Monad Transformers: We can utilize monad transformers when working with nested or multiple monads in the same context. Transformers, such as
EitherTorOptionT, help manage the complexity of combining different monads and allow for more straightforward and readable code.
4.5 Use cases
There are multiple use cases for monads, mainly but not exclusively around error handling.
The monadic approach has many use-cases, and below are five examples:
- Handling Null Values: The Option monad can be used to handle null values in a more functional and type-safe manner, avoiding
NullPointerExceptionsand improving code robustness. - Asynchronous Operations: The Future monad can represent asynchronous computations, such as network requests or file I/O, simplifying the control flow and enabling the chaining of operations.
- Error Handling: The Either monad can be used to represent computations that may fail, allowing for structured and type-safe error handling and reducing the risk of runtime errors.
- Composing Functions: Monads like Option, Either, or Future can simplify the control flow when composing multiple functions, making the code more expressive and easier to read and maintain.
- Stateful Computations: The State monad can represent stateful computations in a functional and immutable way, avoiding mutable state and enhancing code modularity and composability.
5. Pattern matching and extractors
The concept of pattern matching has been used in various forms in different programming languages and systems. Still, its specific use in functional programming is often attributed to the computer scientist David Turner.
Turner also invented the functional programming language Miranda, which was one of the first languages to incorporate pattern matching as a core feature. It was introduced in the 1980s and used a syntax for pattern matching that has since become a common feature in many functional programming languages, including Haskell, F#, and Scala.
The concept of extractors is also often attributed to David Turner, who introduced them as a feature of the same language.
5.1 Definition
Pattern matching is a useful technique that allows us to match values against patterns and execute different code blocks depending on the match result. To perform pattern matching in Scala, we use the match keyword followed by a sequence of cases that match against patterns. Each case specifies a pattern to match against and an associated code block to execute if the pattern matches.
Pattern matching is often used with case classes, sealed traits, tuples, and lists and provides a concise and expressive way to deconstruct data structures and handle different cases.
Here is the basic syntax of a pattern-matching construct:
Code
// Define a pattern-matching construct
def patternMatch(x: Int): Unit = {
x match {
case 14 => println("The number is 14")
case 15 => println("The number is 15")
case _ => println("The number is not 15 nor 16")
}
}
// Define simple integer variables
val simple_int_1: Int = 14
val simple_int_2: Int = 15
val simple_int_3: Int = 16
// Call function
patternMatch(simple_int_1)
patternMatch(simple_int_2)
patternMatch(simple_int_3)Output
// The number is 14
// The number is 15
// The number is not 15 nor 165.2 Advantages
The main advantage of pattern matching is probably their capacity to handle complex patterns in expressions. Additionally, type-checking is made easier than using a conventional if - else if - else construct. However, pattern-matching is such an important concept in functional programming that there are plenty more advantages:
- Conciseness: Pattern matching allows us to express complex conditional logic more concisely and expressively. This can help reduce the amount of boilerplate code and make our code more readable and maintainable.
- Type safety: Pattern matching is type-safe and helps catch errors at compile-time rather than runtime. This can help avoid bugs and improve the overall reliability of our code.
- Destructuring: Pattern matching allows us to destructure data structures, such as case classes or tuples, and extract values from them. This can make our code more modular and reusable.
- Extensibility: Pattern matching is extensible, allowing us to add new patterns and match against new data types as needed. This can help make our code more flexible and adaptable to changing requirements.
- Compatibility with functional programming: Pattern matching is a fundamental feature of functional programming, and Scala’s support for pattern matching makes it a natural fit for functional programming paradigms. This can help make our code more composable and easier to reason about.
5.3 Examples
In our last technique, we used the Option monad to implement two safe division functions that can deal with undefined values (i.e., division by zero).
In our first example, we’ll add more functionalities to this implementation.
5.3.1 Handling an undefined operation
We can extend our safeDivision functionality by using pattern matching:
Code
def checkDivide(result: Option[Double]) = {
result match {
case Some(value) => println(s"Division result: $value")
case None => println("Division by zero is not allowed")
}
}Now, we simply feed our expression:
Code
checkDivide(safeDivOne(safeDivTwo, 12, 2, 3))
checkDivide(safeDivOne(safeDivTwo, 12, 0, 3))Output
// Division result: 2.0
// Division by zero is not allowed5.3.2 Matching an animal species
Let us create a simple application that takes an input string representing an animal’s name and, using pattern matching, determines the animal’s classification within a basic hierarchy. The hierarchy consists of 3 levels: Mammal, Bird, and Reptile. We must match the input animal to the correct classification and return the correct class as a String.
Code
// Define an animal checker
def checkAnimal(animal: String): String = {
animal match {
case ("Elephant" | "Whale" | "Dog") => "Mamal"
case ("Parrot" | "Eagle" | "Penguin") => "Bird"
case ("Lizard" | "Tortoise" | "Snake") => "Reptile"
case _ => "Animal is not in DB, sorry."
}
}
// Define an animal
val my_animal = "Snake"
// Call function
checkAnimal(my_animal)Output
res1: String = "Reptile"5.3.3 Matching a data type
Let us define a function that checks for four basic base data types in Scala. The function accepts a value x and returns the corresponding type as String.
For this example, we’ll define two versions of the same function: one using pattern matching and the other using if-else if-else constructs.
Code
// Implement using pattern matching
def checkType1(x: Any): String = x match {
case _: Int => "Int"
case _: String => "String"
case _: Boolean => "Boolean"
case _ => "Unknown"
}
// Implement using a if-else constructs
def checkType2(x: Any): String = {
if (x.isInstanceOf[Int]) "Int"
else if (x.isInstanceOf[String]) "String"
else if (x.isInstanceOf[Boolean]) "Boolean"
else "Unknown"
}
// Call functions
checkType1(1)
checkType2(1)
checkType1("A String")
checkType2("A String")While both implementations return the same value, the first function is much more concise and readable since we use a placeholder _. In contrast, the second one requires additional methods to do the same.
Output
res1: String = "Int"
res2: String = "Int"
res3: String = "String"
res4: String = "String"5.3.4 Extractors with a custom class
Let us define a custom class called PositiveInt, which can represent a positive integer object. We want to be able to check if an integer is positive by using the PositiveInt constructor and pattern matching.
Code
// Define our custom class
class PositiveInt(val value: Int)
// Define an object
object PositiveInt {
def unapply(value: Int): Option[PositiveInt] =
if (value > 0) Some(new PositiveInt(value)) else None
}
// Define a checker that includes an extractor
def checkNum(x: Int) = x match {
case PositiveInt(positiveInt) => println(s"The number ${positiveInt.value} is positive.")
case _ => println(s"The number ${x} is not positive.")
}
checkNum(7)
checkNum(-10)Output
// The number 7 is positive.
// The number -10 is not positive.Let us explain our algorithm in more detail:
- We declare a class
PositiveInt, which accepts an integer value. - We declare a companion object,
PositiveInt, which will contain (encapsulate) the extractor method usingunapply. This will destructure an object belonging to thePositiveIntclass and extract its value. If our object is not a positive integer, it will returnNone, and the pattern-matching implementation will catch it. - We define a pattern-matching implementation that calls the
PositiveIntclass with a variablepositiveIntthat will hold the deconstructedPositiveIntvalue if it’s positive.
5.4 Recommendations & best practices
- Covering all cases: We must cover all possible cases in pattern-matching expressions by using a wildcard pattern (
case _ =>) as a catch-all for unexpected cases. This helps avoid missing cases and keeps the code robust. - Eliminating type checks and casts: We can use pattern matching to destructure and match on types instead of using
isInstanceOfandasInstanceOf, as it leads to cleaner and safer code. - Using sealed traits and case classes: We can favor using sealed traits and case classes when working with algebraic data types, as sealed traits enable exhaustiveness checks, and case classes provide built-in support for pattern matching, immutability, and useful methods like
copyandequals. - Creating extractor objects and unapply methods: We can use extractor objects and
unapplymethods (orunapplySeqfor sequences) to create custom data structures or classes that facilitate pattern matching. This allows for easy destructuring and value extraction, similar to case classes. - Prioritizing simplicity and maintainability: We can organize pattern-matching expressions for readability and avoid overly complex patterns that can be hard to understand. This helps keep the code simple and maintainable.
5.5 Use cases
At this point, it would be valid to ask ourselves why to use match if we already have an if-else if-else construct.
We saw a very simple example, but logical tests can increase in size and include complex patterns that we must match. In this case, a pattern-matching approach simply provides better readability. Also, logical tests can include complex data structures such as multidimensional arrays; pattern matching is optimized to handle those.
As we already saw, pattern matching supports a simplified syntactic construct for type checking; this is extremely useful if we’re working with custom or base types.
So, some rules would include the following:
- If we have a simple logical test we’d like to perform, we use an
if-elseconstruct. - If we have a more complex set of logical rules, we use pattern matching.
- If we wish to perform type checking, we use pattern matching.
What about extractors? As we might suspect, most applications involve some type of value extraction from a given class to check something or operate with something else:
- Parsing strings: We can extract specific components from formatted strings, such as email addresses, URLs, or date formats.
- Destructuring custom data structures: We can also simplify access to nested values or elements in complex data types.
- Type-based pattern matching: We can match and extract values based on their types, eliminating the need for explicit type checking and casting.
- Matching expressions with additional conditions: As we saw in our last example, we can apply custom logic or constraints during pattern matching, making match expressions more expressive.
- Simplifying complex pattern matching: We can create more readable and maintainable pattern-matching expressions by encapsulating custom matching logic in extractors.
6. Lazy evaluation
The concept of lazy evaluation has been around for a long time and has been used in various forms in different programming languages and systems. However, the term “lazy evaluation” was coined in the 1970s by the computer scientist Peter J. Landin in his paper “The Next 700 Programming Languages“.
It was also highly influenced by Daniel Friedman and David Wise in their paper “Cons should not evaluate its arguments“.
6.1 Definition
Lazy evaluation is an extremely important concept, specifically (but not exclusively), in the context of big data processing pipelines. Lazy evaluation or call-by-need is an evaluation strategy where an expression isn’t evaluated until its first use (i.e, to postpone the evaluation till it’s demanded).
6.2 Advantages
There are plenty of advantages when working with evaluation. Below, we list 5 of them:
- Improved performance: Delaying the computation of expensive operations until they are actually needed can improve performance, reducing unnecessary computations and memory usage.
- Avoidance of infinite computations: Lazy evaluation can help prevent infinite computations by only computing values as they are needed, preventing stack overflows and other errors.
- Better resource management: Lazy evaluation can improve resource management by only allocating resources when needed, reducing memory usage, and improving overall performance.
- Control flow management: Lazy evaluation allows for better control flow by specifying the order of computations, leading to more concise and readable code.
- Compatibility with functional programming: Lazy evaluation is a core feature of functional programming, and Scala’s support makes it well-suited for functional programming paradigms, making code more modular and composable.
6.3 Examples
If we’ve followed this article from the start, we might have noticed that all the functions we implemented are evaluated eagerly every time they’re called. This means the function is executed, and its result is computed each time we invoke it.
We can, however, declare a lazy value by using the lazy keyword:
6.3.1 Defining a simple lazy value
Let us declare two simple variables: An eager variable and a lazy one:
Code
// Define an eager list and a lazy list
val my_list:List[Int] = List(1, 2, 3, 4, 5)
lazy val my_lazy_list:List[Int] = List(1, 2, 3, 4, 5)If we hover over the variable name, we will see that the eager variable already returns its value, while the second does not:
Output
my_list: List[Int] = List(1, 2, 3, 4, 5)
lazy private val my_lazy_list: List[Int]While we can define lazy values, the same does not apply to functions; functions are eagerly evaluated by default and can’t be made lazy like vals can using the lazy keyword.
However, we can achieve a lazy evaluation of function results by returning a lazy val or using memoization techniques to cache the function results.
6.4 Recommendations & best practices
- Using
lazyjudiciously: Whilelazyvalues can help reduce computational overhead, they can also increase complexity and the potential for bugs. It is important to uselazyonly when necessary and to remember that it may introduce unexpected behavior, such as initialization order issues. - Avoiding side effects: It is important to avoid using
lazyvalues with side effects, as their evaluation is not guaranteed to occur exactly once. Side effects can also introduce unexpected behavior, such as race conditions and thread-safety issues. - Memoizing expensive computations: Memoization techniques should be used to cache the results of expensive computations in
lazyvalues. This can help improve performance by avoiding recomputing the same result multiple times. - Limiting scope: The scope of
lazyvalues should be limited to where they are needed, as they may introduce additional memory overhead. Defininglazyvalues at the top level or in long-lived objects should be avoided, as their memory may be retained longer than necessary. - Being mindful of serialization: It is important to remember that
lazyvalues may not serialize properly and need to be manually re-initialized after deserialization. If objects containinglazyvalues need to be serialized, it is important to ensure they are properly initialized before serialization.
6.5 Use cases
As we might suspect, lazy evaluation is useful when we want to optimize a given application’s performance and memory usage. Again, this is especially important when working with big data. However, that’s far from being the only potential application:
- Initialization-on-demand: Lazy evaluation can be used to defer the initialization of values until they are needed. This can help reduce overhead and improve performance by only computing values as they are needed.
- Memoization: Lazy evaluation can be used for memoization, which involves caching the results of expensive computations in a
lazyvalue. This can help improve performance by avoiding recomputing the same result multiple times. - Thread-safe lazy initialization: Lazy evaluation can be used to implement thread-safe initialization of objects or resources by using
lazyvalues with synchronized blocks or other synchronization mechanisms. - Lazy loading: Lazy evaluation can be used for lazy loading, where resources such as configuration files, data sets, or images are loaded only when they are actually needed. This can help reduce memory usage and improve performance.
- Circular dependencies: Lazy evaluation can be used to break circular dependencies between objects or classes by using
lazyvalues. This can help avoid initialization order issues and improve the modularity of the code.
7. Implicits and type classes
Implicits and type classes are two different but closely-related concepts widely used in functional programming languages, particularly in Scala. While developing these concepts was a collaborative effort among many programmers and researchers, the contributions of Martin Odersky, the creator of Scala, were particularly significant.
7.1 Definition
Implicits are a way of implicitly passing values, objects, or functions as arguments to a method or function call
The implicit system in Scala allows the compiler to adjust code using a well-defined lookup mechanism. We can leave out information the compiler will attempt to infer at compile time. The Scala compiler can infer one of two situations:
- When a method call or constructor with a missing parameter.
- When we have a missing conversion from one type to another type. This also applies to method calls on an object requiring a conversion.
The compiler converting types to ensure that an expression compiles can be more dangerous. In both situations, the compiler follows a set of rules to resolve missing data and allow the code to compile. When we leave out parameters, it’s incredibly useful and is done in advanced Scala libraries.
Type classes, on the other hand, are a way of defining a set of operations or behaviors that can be applied to a type or class without modifying the type or class itself. In simpler terms, type classes enable us to make a function more ad-hoc polymorphic without touching its code.
If we’ve already used type classes in Python (by employing the @ annotation), then we are already familiar with this concept.
In Scala, things are similar.
7.2 Advantages
Regarding implicits, there are many advantages if used properly:
- Extension methods: Implicits can be used to define new methods for existing types or classes without modifying their original code.
- Type-safe DSLs: Implicits can be leveraged to create type-safe, expressive, user-friendly domain-specific languages.
- Implicit conversions: Implicits can be used to create automatic type conversions, reducing the need for explicit type casting and making the code more readable.
- Type inference: Implicits can aid the compiler in inferring types, leading to less verbose and more maintainable code.
- Flexible API design: Implicits can be used to design flexible and extensible APIs, allowing users to customize or extend the API without altering the underlying source code.
Regarding type classes, the main advantages go around designing polymorphic functions that can inherit a full set of traits from another class. This, of course, provides a valuable tool for promoting code modularization and reusability.
7.3 Examples
Working with implicits requires a lot of practice and expertise in type definition and type behavior since they’re one of the features that, if misused, can drastically reduce the quality of our code by introducing bugs and increasing build and execution times. However, there are plenty of use cases we can explore.
Type classes also require a fair amount of practice; if we’re not careful, we can end up with virtually unintelligible code and impossible to decipher. Also, we can introduce unwanted side effects, a characteristic that functional programming tries to avoid at all costs.
Let us define a very simple example.
7.3.1 Finding an integer
Let us declare a function that accepts an integer value and returns the same value. We’ll define its parameter as implicit and study its behavior.
Code
// Define a function with implicit parameter x
def findInt(implicit x: Int) = x
// Call function without argument
findIntAs expected, we get an error:
Output
could not find implicit value for parameter x: IntThis is because we have not yet declared an implicit value that falls under the scope of the implicit parameter lookup. Let us do that:
Code
// Define a function with implicit parameter x
def findInt(implicit x: Int) = x
// Define an implicit value
implicit val my_int: Int = 10
// Call function without argument
findIntOutput
res1: Int = 10Surprise, surprise, the function gets magically evaluated. What happened was close to magic but not quite magic; we defined a value my_int under the implicit scope. The set of rules for implicit values in the Scala compiler then looked for this value and found one that matched the required type Int.
What if we declare another implicit Int?
Code
// Define a function with implicit parameter x
def findInt(implicit x: Int) = x
// Define two implicit values
implicit val my_int: Int = 10
implicit val my_int_2: Int = 7
// Call function without argument
findIntOutput
ambiguous implicit values:
both value my_int_2 in class MdocApp of type => Int
and value my_int in class MdocApp of type => Int
match expected type IntWe will get an ambiguous implicit value error: since both values belong to the same scope, the compiler does not know which value to evaluate the function with.
But what if, in turn, we declare a value of a different type?
Code
// Define a function with implicit parameter x
def findInt(implicit x: Int) = x
// Define an implicit value
implicit val my_int: Int = 10
implicit val my_string: String = "A String"
// Call function without argument
findIntOutput
res1: Int = 10This works perfectly because our second implicit value, my_string, is not of the required type, and the Scala compiler knows that.
7.3.2 Value formatter
Let us define a type class to format different types when printing them to stdout. We want to be able to use two types: String and Int.
Code
trait Formatter[T] {
def format(value: T): String
}
// Define a Formatter object, including two
// implicit objects: String and Int
object Formatter {
implicit object IntFormatter extends Formatter[Int] {
def format(value: Int): String = s"The integer value is $value"
}
implicit object StringFormatter extends Formatter[String] {
def format(value: String): String = s"The string value is $value"
}
}
// Define the formatter method
def printFormatted[T](value: T)(implicit f: Formatter[T]): Unit = {
println(f.format(value))
}
// Format an int and a string
printFormatted(777)(Formatter.IntFormatter)
printFormatted("a string")(Formatter.StringFormatter)Let us explain in more detail what we just declared:
- We define a type class using
trait. Traits are like templates for classes in Scala. They define a set of methods and fields that can be mixed in to a class to provide additional functionality without requiring the class to inherit from a specific superclass. - We define an object,
Formatter, that will encapsulate two implicit objects:IntFormatterandStringFormatter, one for each type. - We declare a method for each case:
- We mark both formatter objects as
implicit, meaning they can provide a defaultFormatterinstance forStringandIntvalues. - We extend the functionality of
Formatterwith these two methods.
- We mark both formatter objects as
- We then create a function to print the formatted type.
Output
// The integer value is 777
// The string value is a stringWe can look at it this way:
- What do the two printing statement results have in common?
- They accept a value and print it as a string. This is what the
traitdoes. - What is the main difference between
IntFormatterandStringFormatter? - They format the string differently before printing it to
stdout.
We can thus say that the IntFormatter and StringFormatter have effectively extended the functionality of Formatter, which provides a base template of the printing method for both types.
It would be of huge surprise to us that Scala has this incredible feature. The thing is that Scala combines the best of both worlds: Functional & OOP programming.
7.4 Recommendations & best practices
As with any powerful abstraction technique, there are some best practices we can use to avoid Fauda.
- Making sure class type names are clear and concise: We should choose names that accurately describe the purpose of the class and follow standard Scala naming conventions.
- Being able to define class type parameters in a way that makes the class more generic and reusable: We can use type parameters to define generic behaviors and interfaces that different types can use.
- Encapsulating class state and behavior to maintain abstraction and modularity: We can use private and protected modifiers to restrict access to internal class details and expose a public API for interaction with the class.
- Using case classes for immutable data structures: Case classes are designed to provide a convenient and efficient way to define immutable data structures and have built-in support for pattern matching and equality testing.
- Making sure class types are composable and interoperable: We can use traits and mixins to define reusable behaviors that can be mixed in to different class types and adhere to standard Scala conventions for interoperability with other libraries and frameworks.
7.5 Use cases
- Implementing data models for complex applications: Class types are a natural way to represent complex data structures and relationships between entities in an application.
- Defining reusable behavior for different classes: We can use traits and mixins to define reusable behaviors that can be shared among different class types, promoting code reuse and modularity.
- Creating custom collections and data structures: We can use class types to define custom collections and data structures that meet the specific needs of our application, such as efficient lookup or specialized iteration behavior.
- Implementing stateful and event-driven applications: Class types can model stateful entities and represent events and actions that change the application’s state.
- Interacting with external systems and libraries: We can use class types to define data structures and interfaces for interacting with external systems and libraries, promoting interoperability and encapsulating external dependencies.
8. Continuation-passing style (CPS)
The concept of CPS can be traced back to the work of several computer scientists, including John McCarthy, Peter Landin, and Christopher Strachey.
However, the specific term “continuation-passing style” and its use in programming languages can be attributed to the American computer scientist Daniel P. Friedman and his colleagues.
8.1 Definition
This one is tricky to define without any previous context of what continuation is. Because of this, we’ll first define a few concepts that will be useful.
8.1.1 Continuation
A continuation is a primitive construct to abstract control flow. It represents a point in time of a given execution flow. A continuation usually consists of two states:
- The program state at a given point in time.
- The remaining code to run.
So, in simpler terms, if we’re executing a program and we define a breaking point in a given line, we save a picture of the program at that particular point in time.
The remaining code to be run is also saved as part of the snapshot.
8.1.2 Continuation-passing style (CPS)
CPS is simply a way to implement continuations in a program. More formally, CPS is a way of writing programs that has proven useful as an intermediate form of compiling functional languages. By using CPS, things like the order of evaluation and temporary variables are made explicit. We must remember that CPS is simply a programming style that can be adopted by mixing it with other styles; using one CPS implementation does not mean we require our entire code to work that way.
Thinking in terms of functional programming, we know that the main way to abstract a computation is by using functions and their variations. Defining a CPS as a function that abstracts continuation would make sense.
This concept is confusing. If we don’t yet know where we’re going, that’s OK. However, what we ultimately want, is to control the control flow.
Let us think of a more concrete example where we would like to define two functions: The first one will add two integer values, and the second one will calculate the product of the result with another integer value we designate.
We’ll start with the conventional style:
Code
// Define an addition function
def addInts(x: Int, y: Int): Int = {
x + y
}
// Define a multiplication function
def multiplyInts(d: Int, z: Int): Int = {
d * z
}
// Declare test variables
val x1 = 7
val y1 = 14
val z1 = 21
// Call both functions
println(s"($x1 + $y1) * $z1 = ${multiplyInts(addInts(x1, y1), z1)}")Output
// (7 + 14) * 21 = 441Simple, right?
Now, let us define an equivalent implementation using the CPS style:
Code
// Define an addition function
def addIntsCPS(x: Int, y: Int, k: Int => Unit): Unit = {
k(x + y)
}
// Define a multiplication function
def multiplyIntsCPS(d: Int, z: Int, k: Int => Unit): Unit = {
k(d * z)
}
// Declare test variables
val x2 = 7
val y2 = 14
val z2 = 21
addIntsCPS(x2, y2, sum => {
multiplyIntsCPS(sum, z2, product => {
println(s"($x2 + $y2) * $z2 = $product")
})
})Let us explain step by step:
- We define an addition function,
addIntsCPS, which now takes one additional argument,k. This additional argument is our continuation function. - The
addIntsCPSalso accepts two integers but does not return the value to the execution process. Instead, it returns it to another function (i.e., the continuation function). - The exact same happens with
multiplyIntsCPS. - We then define values to use in our call.
- We call
addIntsCPSwith ourIntarguments but also include a call to the anonymous continuation function usingsumas an argument (kaccepts anInt, and returns aUnit) - The continuation function receives the
sum, then callsmultiplyCPSwith thesum,z, and another continuation function that takes the product as its argument. - Inside the
multiplyCPSfunction,sum * zis calculated, and the result is passed to the next continuation function. - The last continuation function receives
productand sends the result toprintln.
As expected, we get the same result:
Output
// (7 + 14) * 21 = 441If we noticed, this mechanism provided us with a way to control the flow of the process, but it also provided a funny syntax. This type of syntax is well known in a wide variety of languages and is sometimes referred to as callback hell in the context of JavaScript, but it really applies to any language dealing with functions.
In short, CPS has many advantages, but its abuse can lead to poor syntax.
8.2 Advantages
If we are to implement such a concept, it must have some great advantages, right? Yes, CPS has plenty of use cases we can explore. We can mention some of them:
- Improving control flow: CPS makes the control flow of our program explicit, making it easier to understand and manage, especially in asynchronous scenarios.
- Chaining operations: CPS allows us to chain multiple operations by passing the continuation functions as arguments, improving code readability.
- Tail-call optimization: CPS can enable tail-call optimization in languages that support it, which can help avoid stack overflow errors in deep recursion.
- Non-blocking code: CPS is well-suited for non-blocking and asynchronous programming, as it avoids blocking calls and promotes efficient resource usage.
- Enhancing modularity: CPS promotes modular code design by using continuation functions, making it easier to extend, maintain, and debug our code.
8.3 Examples
Let us go over one additional example to further clarify the CPS style:
8.3.1 Algebraic calculations on lists of integers
Let us imagine a scenario where we have a list of integers, and we want to calculate the sum and product of all elements in the list, but we want to use CPS to break the problem into smaller parts.
Let us start by defining what we’ll need to achieve this:
- A
sumListCPSfunction that will perform a sum operation on a list of integers and will return the result to a continuation functionk. - A
productListCPSfunction that will perform a product operation on a list of integers and will return the result to a continuation functionk. - A list of
Intvalues. - A call to the CPS functions we defined previously.
Code
def sumListCPS(list: List[Int], k: Int => Unit): Unit = k(list.sum)
def productListCPS(list: List[Int], k: Int => Unit): Unit = k(list.product)
val numbers = List(7, 14, 21, 28, 35)
sumListCPS(numbers, sum => {
println(s"Sum: $sum")
productListCPS(numbers, product => {
println(s"Product: $product")
})
})Output
// Sum: 105
// Product: 20168408.4 Recommendations & best practices
As with many of the concepts we’re reviewed in this segment, CPS is a technique that, if used right, can bring a lot of advantages. On the contrary, if misused or abused, it can reduce the quality of our code and introduce unnecessary bugs. Below are some recommendations when dealing with CPS in functional programming:
- Using function composition: We can compose CPS functions using higher-order functions to create reusable and modular code, improving readability and maintainability.
- Using tail-recursive CPS functions: We should aim to write tail-recursive CPS functions when dealing with recursion. It enables tail-call optimization and prevents stack overflow errors in supporting languages.
- Using meaningful continuation names: We must choose descriptive names for continuation functions to improve code readability and make it easier to understand the purpose and flow of each continuation.
- Using type annotations: We can improve code clarity and maintainability by adding type annotations to CPS functions and their continuation arguments, making understanding the expected input and output types easier.
- Using CPS selectively: We must evaluate whether CPS is the best solution for a given problem, as CPS might not be the optimal choice for simple, non-asynchronous scenarios. In such cases, conventional programming styles might be more suitable and produce more readable code.
8.5 Use cases
CPS, and continuation, in particular, are vast subjects with many variations we can implement. However, we can mention some real-world use cases:
- For asynchronous programming: We can manage complex operations by chaining multiple callbacks, avoiding callback hell, and improving code readability.
- In compilers and interpreters: We can leverage CPS for implementing language features like exception handling, garbage collection, and concurrency in compilers and interpreters.
- For state machines: We can model state machines with CPS by representing different states as continuation functions, providing a clear and modular way to handle state transitions.
- For cooperative multitasking: We can apply CPS to implement cooperative multitasking, where tasks voluntarily yield control by calling their respective continuation functions, improving resource usage and scheduling.
- For backtracking algorithms: We can use CPS to implement backtracking algorithms, enabling efficient exploration of potential solutions and making it easier to revert to previous states when a solution is not found.
9. Futures and Promises
Futures and promises are concepts used in computer science and programming languages for many years. They are particularly popular in functional programming languages used for asynchronous and concurrent programming.
The concept of futures was first introduced in the 1970s by Barbara Liskov and Alan Snyder, who proposed a mechanism for specifying and manipulating computations that had not yet completed. In their paper, they described a programming construct called a “future” that represented the result of a computation that would be available at some point in the future.
Promises were introduced later as a way to represent the other side of the future relationship: the computation that produces the result. A promise is an object that represents a value that may not be available yet but will be available at some point in the future. When the value becomes available, the promise is “fulfilled” with the value.
9.1 Definition
As with CPS, it’s worth defining a series of terms to understand Futures & Promises better.
9.1.1 Futures
Futures provide a way to reason about performing many operations in parallel– in an efficient and non-blocking way. A Future is a placeholder object for a value that may not yet exist. Generally, the value of the Future is supplied concurrently and can subsequently be used.
For this definition to make sense, we must also define concurrency and asynchronous processes.
9.1.2 Concurrency
Concurrency means multiple computations are happening at the same time. In a concurrent system, multiple threads of execution can run independently of each other, potentially allowing for increased throughput, responsiveness, and efficiency.
Concurrency is often used in systems that handle multiple requests or perform tasks simultaneously. For example, a web server might use concurrency to handle multiple requests from clients at the same time, or a database might use concurrency to allow multiple queries to be executed concurrently.
9.1.3 Asynchronous processes
Asynchronous processes are processes or operations that do not block or wait for the completion of other processes before proceeding. In an asynchronous process, a request is made, and the process continues to execute while waiting for a response rather than blocking and waiting for the response before continuing.
Asynchronous processes are closely related to concurrency, enabling concurrent execution of multiple tasks without blocking or waiting for completion. By allowing multiple tasks to execute concurrently, asynchronous processes can improve the performance and responsiveness of computer systems, as they can avoid the overhead and delays associated with blocking I/O and waiting for the completion of operations.
9.2 Advantages
Futures and Promises are extremely relevant in many fields. Let us list 5 of them:
- Asynchronous programming: Futures and promises allow us to write asynchronous code simply and concisely. This can help us write more efficient and responsive code that can handle multiple concurrent operations.
- Better error handling: Futures and promises provide a clear and concise way to handle errors and exceptions during asynchronous computations. This can help us write more robust and reliable code, improving the overall quality of our applications.
- Non-blocking I/O: Futures and promises allow us to perform non-blocking I/O operations, freeing up threads and resources to handle other tasks. This can help improve the scalability and performance of our applications.
- Functional composition: Futures and promises are composable and can be used with functional programming constructs, such as
mapandflatMap. This can help us write more concise and expressive code, making it easier to reason about. - Integration with Akka and other libraries: Futures and promises are integrated with Akka, Scala’s actor-based concurrency library, and many other libraries in the Scala ecosystem. This can help us leverage the power of these libraries and write more powerful and expressive code.
9.3 Examples
Let us implement a function that calculates the sum of two integers asynchronously and returns a future that completes when the calculation is done.
9.3.1 One asynchronous calculation
Let us define a function that calculates the sum of two integers asynchronously and returns a future that completes when the calculation is done.
The future will be waiting for the computation value and realize to a value when the computation concludes.
Let us break our approach step-by-step:
- We define a
Promiseassociated with aFuture. This promise will expect an integer value. - We then define an asynchronous task.
- We complete the promise with the result of the calculation.
- We start the task on a separate thread.
- We finally call our asynchronous process using the
AwaitAPI. - The
sumAsyncprocess call will tell us if our process terminated successfully.
Code
import scala.concurrent.{Promise, Await, Future}
import scala.concurrent.duration._
// Define Promise
def sumAsync(a: Int, b: Int): Future[Int] = {
val promise = Promise[Int]()
// Start an asynchronous task to calculate the sum of the integers
val task = new Runnable {
override def run(): Unit = {
val result = a + b
// Fulfill the promise with the result of the calculation
promise.success(result)
}
}
// Start the task on a separate thread
new Thread(task).start()
promise.future
}
// Assign sumAsync to variable
val future = sumAsync(1, 2)
// Call using Await API
val result = Await.result(future, 10.seconds)
println(s"Sum: $result")Output
// future: Future[Int] = Future(Success(3))
// result: Int = 3
// Sum: 3This implementation considered one single calculation, but we can do the same for two calculations.
9.3.2 Two asynchronous calculations
Let us implement an addition and a multiplication asynchronously and returns a future that completes with the result of both operations:
The process will be similar to our previous example. The only difference is that we’ll now use a for comprehension that combines the futures returned by the addAsync and multiplyAsync functions.
Code
import scala.concurrent.Future
import scala.concurrent.ExecutionContext.Implicits.global
// Define operation 1
def addAsync(a: Int, b: Int): Future[Int] = Future {
a + b
}
// Define operation 2
def multiplyAsync(a: Int, b: Int): Future[Int] = Future {
a * b
}
// Define task
val resultFuture = for {
sum <- addAsync(7, 5)
product <- multiplyAsync(7, 5)
} yield (sum, product)
// Call task
val result_2 = Await.result(resultFuture, 10.seconds)Output
// resultFuture: Future[(Int, Int)] = Future(Success((12,35)))
// result_2: (Int, Int) = (12, 35)9.4 Recommendations & best practices
Futures and Promises are quite an elaborate concept that requires sufficient domain knowledge in asynchronous processing and concurrency since a badly implemented process can crash the entire program or introduce vulnerabilities in our code.
Below are some best practices when working with these techniques:
- Improving parallelism for performance: We can also use the
Future.sequencemethod to execute a collection of futures in parallel. TheFuture.sequencemethod will execute all the futures in the collection in parallel and return a future that completes when all the futures have been completed. This can improve performance by allowing multiple tasks to execute concurrently. - Avoiding blocking: When working with futures, it is important to avoid blocking as much as possible. Blocking can cause performance issues, and defeats the purpose of using futures in the first place. Instead of blocking, we can use non-blocking operations and combinators like
map,flatMap,filter, andonCompleteto compose and transform futures. - Handling errors: Futures can fail, so it is important to handle errors properly. We can use the
recoverandrecoverWithmethods to handle errors and return a default value or another future in case of failure. We can also use thefallbackTomethod to try an alternative future in case of failure. - Using
ExecutionContext: When working with futures, it is important to use anExecutionContextto execute the futures. We can use theExecutionContext.Implicits.globalexecution context for simple cases or provide a custom execution context for more complex cases. - Using Promise for more control: Promises provide more low-level control over the completion of futures. We can use promises when we need to create a future that is not immediately available or when we need to complete a future manually.
9.5 Use cases
- Using futures for network calls: When making network calls, it is important to use futures to ensure that the calls do not block the main thread. By using futures, network calls can be made asynchronously, and the result can be returned when it becomes available.
- Using promises for caching: Promises can be used for caching values that are expensive to compute. By creating a promise and computing the value asynchronously, subsequent calls can be immediately satisfied by returning the cached value without recomputing it.
- Using futures for parallelism: Futures can be used to execute tasks in parallel, allowing multiple tasks to execute concurrently. This can be useful for applications that require high-performance processing of large data sets.
- Using promises for inter-thread communication: Promises can be used for communication between threads, allowing one thread to signal another when a value becomes available. This can be useful for implementing thread-safe data structures and synchronization primitives.
- Using futures for user interface updates: Futures can be used to perform background processing and update the user interface when the processing is complete. By using futures to perform background processing, the user interface remains responsive and can provide feedback to the user during the processing.
10. Higher-kinded types
We close this segment with a very interesting and special group of types called higher-kinded types. Their use as a feature of functional programming is often attributed to the computer scientist and programming language designer Philip Wadler and was formally introduced in computational theory in the ML language during the late 1970s.
10.1 Definition
Higher-kinded types, also known as type constructors or type-level functions, are a type-level abstraction that allows type constructors (such as lists or trees) to be parameterized by other type constructors.
Let us imagine a tool that can drill a hole in any kind of material, such as wood, metal, or plastic. This tool would be analogous to a higher-kinded type since it can work with different types of materials. In simpler terms, higher-kinded types are a way of defining types that can work with other types.
In programming, higher-kinded types are used to create types that work with other types, like lists, maps, and other data structures. This makes these types more generic and reusable and makes it easier to write code that works with different types of data.
10.2 Advantages
As with many elegant forms of abstraction, the advantages of this technique are vast:
- Library Design and Implementation: Most use cases of higher-kinded types are found in library design and implementation. Scalaz, one of the most popular Scala projects, uses higher-kinded types to extend the core Scala library for functional programming. It gives the client more control over the exposed interfaces while reducing code duplication.
- Reusability: Higher-kinded types allow for creating more generic and reusable abstractions, making writing code that works with different types of data easier.
- Flexibility: They also make it easier to create complex data structures and algorithms that can work with different data types.
- Separation of concerns: They allow for a clear separation of concerns between the data and the operations that work on that data, making code easier to understand and maintain.
- Modularity: Higher-kinded types enable the creation of modular and composable code that can be easily combined and reused in different contexts.
- Type safety: Finally, higher-kinded types can help prevent type errors and make it easier to reason about code by ensuring that types are used correctly and consistently throughout a program.
- Polymorphic Containers: Higher-kinded types are useful when we want to create a container that can hold any type of item; we don’t need a different type for each specific content type.
Let us work on an example to further clarify.
10.3 Examples
Since higher-kinded types are somewhat of a difficult topic without some prerequisites, we’ll stick with an extremely simple case of a higher-kinded type for a specific container type, in our case, a List or an Option.
10.3.1 Implementing a higher-kinded type for a List
Before any code, we’ll explain step-by-step what we will do:
- Define the higher-kinded type called Box: Define a trait or abstract class with a type parameter that itself takes a type parameter. This is our higher-kinded type.
- Define how the Box trait should work with Lists: It defines how the methods in the
Boxtrait should behave when working with aList. In our case, theListBoxclass will provide an implementation of thefirstmethod for aList. - Define how the Box type should work with Vectors: The
VectorBoxclass will provide an equivalent implementation for vectors. - Implement a function that can work with instances of both types: Implement a function
findFirstthat works with instances of our higher-kinded type.
Now that we have a little bit more clarity, we can begin with our implementation:
Code
// 1. Define the higher-kinded type called Box
trait Box[F[_]] {
def first[A](fa: F[A]): Option[A]
}
// 2. Define how the Box type should work with Lists
class ListBox extends Box[List] {
def first[A](list: List[A]): Option[A] = list.headOption
}
// 3. Define how the Box type should work with Vectors
class VectorBox extends Box[Vector] {
def first[A](vector: Vector[A]): Option[A] = vector.headOption
}
// 4. Implement a function findFirst that works with instances of our higher-kinded type
def findFirst[F[_], A](box: Box[F], container: F[A]): Option[A] = {
box.first(container)
}
// 5. Create an instance of ListBox and use it to find the first element in a list
val listBox = new ListBox()
val myList = List(1, 2, 3)
val firstElementList = findFirst(listBox, myList)
// 6. Create an instance of VectorBox and use it to find the first element in a Vector
val vectorBox = new VectorBox()
val myVector = Vector(4, 5, 6)
val firstElementVector = findFirst(vectorBox, myVector)Code
// Print both values
println(firstElementList)
println(firstElementVector)Output
// Some(1)
// Some(4)We can even go one step further and introduce a generic implementation of the Box trait to handle different container types based on the type constructor provided. However, we will need to introduce two new concepts and one curious library called Cats (yes, there are actual cats in Cats), aimed at providing abstractions for Scala.
For this, we will first head to our build.sbt file and append the following line:
Code
libraryDependencies += "org.typelevel" %% "cats-core" % "2.6.1"So that our entire build file should look like such:
Code
import Dependencies._
ThisBuild / scalaVersion := "2.12.8"
ThisBuild / version := "0.1.0-SNAPSHOT"
ThisBuild / organization := "com.example"
ThisBuild / organizationName := "example"
lazy val root = (project in file("."))
.settings(
name := "10-advanced-programming-techniques",
libraryDependencies += scalaTest % Test,
libraryDependencies += "org.typelevel" %% "cats-core" % "2.6.1"
)This should automatically download Cats and make it available for import. So, back in our worksheet file, we can include the following:
Code
import cats._
import cats.implicits._
import cats.instances.list._
import cats.instances.vector._Lets get this party started, shall we?
Let us define our generic implementation:
Code
class GenericBox[F[_]: Foldable] extends Box[F] {
def first[A](container: F[A]): Option[A] = {
Foldable[F].reduceLeftOption(container)((a, _) => a)
}
}Where:
Foldableis a type-class in theCatslibrary representing data structures that can be folded to a summary value. It provides a set of methods for folding and reducing data structures, such asfoldLeft,foldRight,reduceLeftOption,reduceRightOption, and more.reduceLeftOptionis a method provided by theFoldabletype-class that reduces a container of elements of typeAto a single value of typeA. It applies a binary function, which takes two elements of typeAand returns a single element of typeAin a left-associative manner.
So, in summary, the combination of Foldable with reduceLeftOption gets us the first element of a List or a Vector, which is exactly what we’re looking for.
Lastly, we simply need to define our appropriate instances and call the appropriate methods:
Code
// 2. Create an instance of ListBox and use it to find the first element in a list
val genericListBox = new GenericBox[List]
val myList2 = List(1, 2, 3)
val firstElementList2 = genericListBox.first(myList2)
// 3. Create an instance of VectorBox and use it to find the first element in a Vector
val genericVectorBox = new GenericBox[Vector]
val myVector2 = Vector(4, 5, 6)
val firstElementVector2 = genericVectorBox.first(myVector2)Code
println(firstElementList)
println(firstElementVector)Output
// Some(1)
// Some(4)So, where did our drill and materials analogy go in all of this nonsense? Simple:
Boxis our marvelous drill.Listis a glass material.Vectoris a stone material.Boxcan drill both (i.e., can get their first element):- Using different drillbits in our original implementation.
- Using the “same” drillbit in our last generic implementation.
The interesting thing is that this is just one level of abstraction. We could think that we could keep doing abstractions over traits, and we would be correct. This is precisely the power of higher-kinded types. Additionally, the Cats library provides a wide variety of tools.
10.4 Recommendations & best practices
- Understanding higher-kinded types: Before using higher-kinded types in our code, it’s important to understand what they are and how they work. This can help us write more efficient and expressive code, making it easier to reason about and maintain.
- Using type bounds: When defining higher-kinded types, we should use type bounds to restrict the range of possible data types. This can help us write more generic and reusable code while ensuring type safety.
- Leveraging type classes: We can use type classes to provide common functionality across different data types. This can help us write more concise and expressive code, making it easier to understand and maintain.
- Using type aliases: We can use type aliases to provide descriptive names for higher-kinded types. This can help us write more readable and expressive code, making it easier to understand and maintain.
- Being aware of performance implications: Higher-kinded types can have performance implications, particularly when used with large data sets. We should be aware of these implications and consider using specialized data structures or algorithms when appropriate.
10.5 Use cases
- Collections: Higher-kinded types are commonly used in Scala collections to provide generic operations that work across different data types. This allows us to write more reusable and easier-to-maintain code.
- Type-safe database access: Higher-kinded types can be used to provide a type-safe and generic interface to a database. This allows us to write more modular and easier-to-maintain code while ensuring type safety.
- Parsing: Higher-kinded types can be used to provide a generic and composable way to parse different data formats, such as JSON or XML. This allows us to write code that is more flexible and easier to maintain while still ensuring type safety.
- Concurrency: Higher-kinded types can be used to provide a type-safe and generic way to handle concurrency in Scala. This allows us to write code that is more scalable and easier to reason about while still ensuring type safety.
- Functional programming: Higher-kinded types are a fundamental feature of functional programming and can be used to provide a generic and composable way to work with functions in Scala. This allows us to write code that is easier to reason about while ensuring type safety.
Next steps
Scala, and functional programming in general, provides a wide variety of advanced (and cryptically-named) techniques and constructs we can use. We must remember that functional programming is heavily based on lambda calculus. Hence, the further we advance, the more mathematical theory will surface.
Additionally, this segment was meant to be a simple introduction, and all concepts included should be further reviewed since they encapsulate key aspects of functional programming.
If we wish to continue our efforts towards more complex programming concepts in Scala, in functional programming, or simply in general programming, we can continue with the following:
- Category Theory: This branch of mathematics provides a solid foundation for understanding functional programming concepts such as Monads, Functors, and Applicative Functors. Studying category theory will help us better comprehend the abstract concepts underlying functional programming.
- Advanced Type Systems: We can dive into more complex type systems, including dependent types, GADTs, and existential types. These advanced type systems can help us express more intricate program properties, enhancing type safety and code maintainability.
- More advanced concurrency models: We should investigate Actor systems, STM (Software Transactional Memory), and stream processing libraries like Akka Streams or FS2. These concepts will help us build highly concurrent and fault-tolerant systems.
- Functional Reactive Programming (FRP): We can learn about FRP and its applications in building responsive, real-time systems. Libraries like
Scala.RxandMonixcan help us explore FRP in Scala. - Lambda Calculus: We should delve into the theoretical foundations of functional programming by studying Lambda Calculus. This will provide insights into the origins of functional programming languages and deepen our understanding of the core principles.
Conclusions
In this segment, we reviewed ten advanced programming techniques in Scala, including tail recursion, higher-order functions, currying, monads, pattern matching & extractors, lazy evaluation, implicits, type classes, continuation-passing style (CPS), and futures & promises. For each technique, we provided a historical introduction, a formal definition, advantages, examples, recommendations & best practices, and use cases.
By learning and implementing these techniques, we have honed our skills as functional programmers and built a strong foundation for tackling even more complex challenges. The next steps outlined above will help us expand our knowledge in functional programming, allowing us to create robust, maintainable, and efficient software solutions.
As we continue to explore advanced concepts and mathematical theories, remember to practice regularly and stay up-to-date with the latest Scala libraries and best practices. As our expertise grows, we’ll be able to leverage the full power of functional programming in Scala to build elegant and sophisticated applications.
References
- Baeldung, Tail vs. Non-Tail Recursion
- Tour of Scala, Higher-Order Functions
- Tour of Scala, Currying
- Towards Data Science, Monads Explained
- Tour of Scala, Extractor Objects
- Scala Tutorial, Lazy Evaluation
- Scala Documentation, Implicit Classes
- Bruchez, Continuations in Scala
- Scala Documentation, Futures and Promises
- Baeldung, Higher-Kinded Types

